
【题目】(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值. 【答案】解:由
的值. 【答案】解:由 ![]() π<x<
π<x< ![]() π,得
π,得 ![]() π<x+
π<x+ ![]() <2π,
<2π,
又cos ![]() =
= ![]() ,∴sin
,∴sin ![]() =﹣
=﹣ ![]() ;
;
∴cosx=cos ![]() =cos
=cos ![]() cos
cos ![]() +sin
+sin ![]() sin
sin ![]() =﹣
=﹣ ![]() ,
,
从而sinx=﹣ ![]() ,tanx=7;
,tanx=7;
故原式= ![]() ;
;
(1)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1 , C1 , F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值. 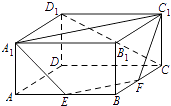
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是圆F1:(x+1)2+y2=16上任意一点(F1是圆心),点F2与点F1关于原点对称.线段PF2的中垂线m分别与PF1、PF2交于M、N两点.
(1)求点M的轨迹C的方程;
(2)直线l经过F2 , 与抛物线y2=4x交于A1 , A2两点,与C交于B1 , B2两点.当以B1B2为直径的圆经过F1时,求|A1A2|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C上的动点M到定点F(1,0)的距离和它到定直线x=3的距离之比是1: ![]() .
.
(1)求曲线C的方程;
(2)过点F(1,0)的直线l与C交于A,B两点,当△ABO面积为 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个匀速旋转的摩天轮每12分钟转一周,最低点距地面2米,最高点距地面18米,P是摩天轮轮周上一定点,从P在最低点时开始计时,则14分钟后P点距地面的高度是米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C: ![]() =1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
=1,点M与曲线C的焦点不重合,若点M关于曲线C的两个焦点的对称点分别为A,B,M,N是坐标平面内的两点,且线段MN的中点P恰好在双曲线C上,则|AN﹣BN|= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< ![]() )的图象与x轴相邻两个交点间的距离为
)的图象与x轴相邻两个交点间的距离为 ![]() ,且图象上一个最低点为M(
,且图象上一个最低点为M( ![]() ,﹣2). (Ⅰ)求f(x)的解析式;
,﹣2). (Ⅰ)求f(x)的解析式;
(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)当x∈[ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com