
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E,F分别是棱AB,BC的中点.证明A1 , C1 , F,E四点共面,并求直线CD1与平面A1C1FE所成角的正弦值. 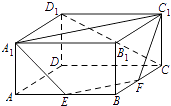
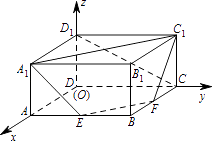
【答案】解:以D为原点建立空间直角坐标系如图所示:
则A1(2,0,1),C1(0,2,1),E(2,1,0),F(1,2,0).D1(0,0,1),
∴ ![]() =(﹣1,1,0),
=(﹣1,1,0), ![]() =(﹣2,2,0).
=(﹣2,2,0).
∴ ![]() =2
=2 ![]() .∵A1 , C1 , E,F四点不共线,
.∵A1 , C1 , E,F四点不共线,
∴A1C1∥EF,
∴A1 , C1 , F,E四点共面.![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =(0,﹣2,1).
=(0,﹣2,1).
设平面A1C1FE的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 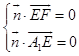 .
.
∴ ![]() ,令z=1得
,令z=1得 ![]() =(1,1,1).
=(1,1,1).
∴cos< ![]() ,
, ![]() >=
>= 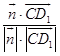 =
= ![]() =﹣
=﹣ ![]() .
.
∴直线CD1与平面A1C1FE所成角的正弦值为 ![]() .
.
【解析】以D为原点建立坐标系,求出 ![]() 和
和 ![]() 的坐标,利用向量共线定理得出四点共面,求出
的坐标,利用向量共线定理得出四点共面,求出 ![]() 和平面A1C1FE的法向量
和平面A1C1FE的法向量 ![]() ,则直线CD1与平面A1C1FE所成角的正弦值为|cos<
,则直线CD1与平面A1C1FE所成角的正弦值为|cos< ![]() ,
, ![]() >|.
>|.
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中边长为1,P、Q分别为BC、CD上的点,△CPQ周长为2. 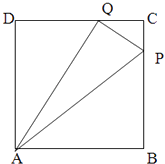
(1)求PQ的最小值;
(2)试探究求∠PAQ是否为定值,若是给出证明;不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线y2=2px(p>0)的焦点,斜率为2 ![]() 的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
的直线交抛物线于A(x1 , y1)和B(x2 , y2)(x1<x2)两点,且|AB|=9,
(1)求该抛物线的方程;
(2)O为坐标原点,C为抛物线上一点,若 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则BB1与平面AB1C1所成的角是( )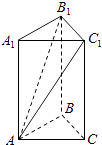
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(﹣3,1),
=(﹣3,1), ![]() =(1,﹣2),
=(1,﹣2), ![]() =
= ![]() +k
+k ![]() (k∈R).
(k∈R).
(1)若 ![]() 与向量2
与向量2 ![]() ﹣
﹣ ![]() 垂直,求实数k的值;
垂直,求实数k的值;
(2)若向量 ![]() =(1,﹣1),且
=(1,﹣1),且 ![]() 与向量k
与向量k ![]() +
+ ![]() 平行,求实数k的值.
平行,求实数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为( ) 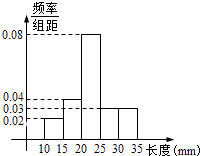
A.20
B.25
C.22.5
D.22.75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若cos ![]() =
= ![]() ,
, ![]() π<x<
π<x< ![]() π,求
π,求 ![]() 的值. 【答案】解:由
的值. 【答案】解:由 ![]() π<x<
π<x< ![]() π,得
π,得 ![]() π<x+
π<x+ ![]() <2π,
<2π,
又cos ![]() =
= ![]() ,∴sin
,∴sin ![]() =﹣
=﹣ ![]() ;
;
∴cosx=cos ![]() =cos
=cos ![]() cos
cos ![]() +sin
+sin ![]() sin
sin ![]() =﹣
=﹣ ![]() ,
,
从而sinx=﹣ ![]() ,tanx=7;
,tanx=7;
故原式= ![]() ;
;
(1)已知函数f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R),若f(x0)=
sinxcosx+2cos2x﹣1(x∈R),若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com