
对于定义域和值域均为 的函数
的函数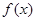 ,定义
,定义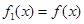 ,
,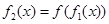 ,…,
,…,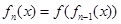 ,n=1,2,3,….满足
,n=1,2,3,….满足 的点称为f的
的点称为f的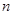 阶周期点.
阶周期点.
(1)设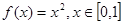 则f的
则f的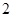 阶周期点的个数是___________;
阶周期点的个数是___________;
(2)设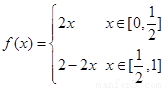 则f的
则f的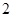 阶周期点的个数是__________ .
阶周期点的个数是__________ .
2,4
【解析】
试题分析:(1)当x∈[0,1]时,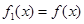 =
=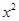 ,由
,由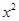 =x得,x=0,1,f的1阶周期点的个数是2;
=x得,x=0,1,f的1阶周期点的个数是2;
当x∈[0,1]时,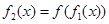 =
=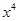 ,由
,由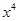 =x,得x=0,1,所以f的
=x,得x=0,1,所以f的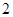 阶周期点的个数是2.
阶周期点的个数是2.
(2)当x∈[0,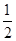 ]时,f1(x)=2x=x,解得x=0,
]时,f1(x)=2x=x,解得x=0,
当x∈(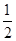 ,1]时,f1(x)=2-2x=x,解得x=
,1]时,f1(x)=2-2x=x,解得x=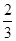 ,∴f的1阶周期点的个数是2;
,∴f的1阶周期点的个数是2;
当x∈[0,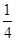 ]时,f1(x)=2x,f2(x)=4x=x,解得x=0;
]时,f1(x)=2x,f2(x)=4x=x,解得x=0;
当x∈(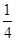 ,
,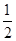 ]时,f1(x)=2x,f2(x)=2-4x=x,解得x=
]时,f1(x)=2x,f2(x)=2-4x=x,解得x=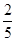 ;
;
当x∈( 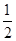 ,
,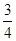 ]时,f1(x)=2-2x,f2(x)=-2+4x=x,解得x=
]时,f1(x)=2-2x,f2(x)=-2+4x=x,解得x=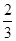 ;
;
当x∈(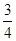 ,1]时,f1(x)=2-2x,f2(x)=4-4x=x,解得x=
,1]时,f1(x)=2-2x,f2(x)=4-4x=x,解得x= .∴f的2阶周期点的个数是22=4.
.∴f的2阶周期点的个数是22=4.
故答案为2,4.
考点:本题主要考查函数的2阶周期点的个数的求法。
点评:新定义问题是中档题.解题时要认真审题,仔细解答,注意分类讨论思想和等价转化思想的灵活运用.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、2n |
| B、2(2n-1) |
| C、2n |
| D、2n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| A、4 | B、6 | C、8 | D、10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com