Question

过抛物线y²=2px（p＞0）的对称轴上一点A（a，0）（a＞0）的直线与抛物线相交于M、N两点，自M、N向直线l：x=-a作垂线，垂足分别为M₁、N₁．
（Ⅰ）当a=时，求证：AM₁⊥AN₁；
（Ⅱ）记△AMM₁、△AM₁N₁、△ANN₁的面积分别为S₁、S₂、S₃，是否存在λ，使得对任意的a＞0，都有S₂²=4S₁S₃成立？若存在，求出λ的值，否则说明理由．

Answer 1

解：依题意，可设直线MN的方程为x=my+a，M（x₁，y₁），N（x₂，y₂），则有M₁（-a，y₁），N₁（-a，y₂）．
将x=my+a代入y²=2px（p＞0）消去x可得y²-2mpy-2ap=0
从而有y₁+y₂=2mp，y₁y₂=-2ap ①
于是x₁+x₂=m（y₁+y₂）+2a=2（m²p+a） ②
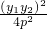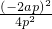又由y₁²=2px₁，y₂²=2px₂可得x₁x₂===a² ③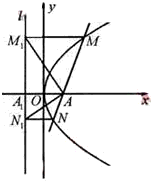
（Ⅰ）证：如图，当a=时，点A（，0）即为抛物线的焦点，
l为其准线，其方程为x=-
此时M₁（-，y₁），N₁（-，y₂）．并由 ①可得y₁y₂=-p²
∵，
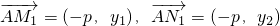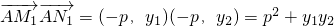∴=0，故有 AM₁⊥AN₁；
（Ⅱ）存在λ=4，使得对任意的a＞0，都有S₂²=4S₁S₃成立，证明如下：
证：记直线l与x轴的交点为A₁，则|OA|=|OA₁|=a．
于是有S₁=|MM₁||A₁M₁|=（x₁+a）|y₁|，S₂=|M₁N₁||AA₁|=a|y₁-y₂|，S₃=|NN₁||A₁N₁|=（x₂+a）|y₂|，
∴S₂²=4S₁S₃?（a|y₁-y₂|））²=（（x₁+a）|y₁|）² ×（（x₂+a）|y₂|）² ?a²[（y₁+y₂）²-4y₁y₂]=[x₁x₂+a（x₁+x₂）+a²]|y₁y₂|
将①、②、③代入上式化简可得
a²（4m²p²+8ap）=4a²p（m²p+2a）上式恒成立，即对任意的a＞0，S₂²=4S₁S₃成立
分析：（Ⅰ） 由题意，可设设直线MN的方程为x=my+a，M（x₁，y₁），N（x₂，y₂），则有M₁（-a，y₁），N₁（-a，y₂）．将x=my+a代入y²=2px（p＞0）消去x可得y²-2mpy-2ap=0利用根与系数的关系及点A（a，0）得出即可证明出结论；
（Ⅱ）假设存在λ=4，使得对任意的a＞0，都有S₂²=4S₁S₃成立，分别表示出三个三角形的面积，代入验证即可证明出结论
点评：本题考查直线与圆锥曲线的综合题，考查了根与系数的关系，三角形的面积公式，抛物线的性质等，解题的关键是认真审题准确转化题设中的关系，本题综合性强，符号计算运算量大，解题时要认真严谨避免马虎出错．