考点：导数在最大值、最小值问题中的应用,函数的最值及其几何意义,函数的零点,平面向量数量积的运算
专题：综合题,导数的概念及应用,平面向量及应用
分析：（1）利用向量的数量积运算和一元二次方程实数根与△的关系即可得出；
（2）利用根与系数的关系，g（a）转化为关于a的函数，利用导数研究函数的单调性即可得出．
解答：
解：（1）由题意知：f（x）=
•
=x
2+（a-3）x+a
2-3a，
∵m、n是方程f（x）=0的两个实根，
∴△=（a-3）
2-4（a
2-3a）≥0，
∴-1≤a≤3．
（2）由题意知：m+n=3-a，mn=a
2-3a，
∴g（a）=m
3+n
3+a
3=（m+n）[（m+n）
2-3mn]+a
3=（3-a）[（3-a）
2-3（a
2-3a）]+a
3=3a
3-9a
2+27，a∈[-1，3]，
故g'（a）=9a
2-18a，
令g'（a）=0，∴a=0或a=2，
从而在[-1，0），（2，3]上g'（a）＞0，g（a）为增函数，
在（0，2）上g'（a）＜0，g（a）为减函数，
∴a=2为极小值点，∴g（2）=15，又g（-1）=15．
∴g（a）的最小值为15．
点评：熟练掌握利用导数研究函数的单调性、极值与最值、一次函数的单调性、一元二次方程的解集与根与系数的关系是解题的关键．
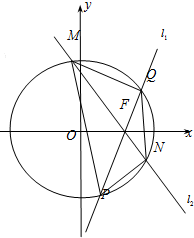已知椭圆
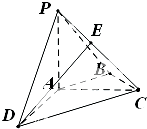如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AB=
已知函数f（x）=Asin（ωx+φ）其中A＞0，ω＞0，0＜φ＜