
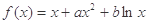 ,曲线
,曲线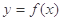 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.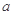 ,
,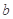 的值;
的值;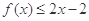 .
. 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:高中数学 来源:不详 题型:解答题
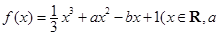 ,
,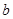 为实数)有极值,且在
为实数)有极值,且在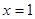 处的切线与直线
处的切线与直线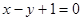 平行.
平行.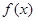 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;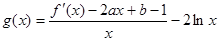 试判断函数
试判断函数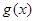 在
在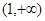 上的符号,并证明:
上的符号,并证明: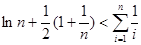 (
(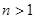 ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。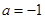 ,求函数
,求函数 的单调区间并比较
的单调区间并比较 与
与 的大小关系
的大小关系 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为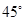 ,对于任意的
,对于任意的 ,函数
,函数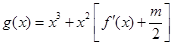 在区间
在区间 上总不是单调函数,求
上总不是单调函数,求 的取值范围;
的取值范围;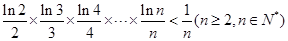 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
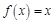 的
的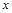 称为
称为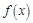 的一阶不动点,符合
的一阶不动点,符合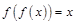 的
的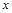 称为
称为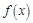 的二阶不动点。设函数
的二阶不动点。设函数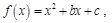 若函数
若函数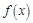 没有一阶不动点,则函数
没有一阶不动点,则函数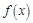 二阶不动点的个数为 ( )
二阶不动点的个数为 ( )| A.四个 | B.两个 | C.一个 | D.零个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com