
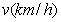 的平方成正比,比例系数为2, 固定部分为3000元.
的平方成正比,比例系数为2, 固定部分为3000元.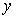 (元)表示为速度
(元)表示为速度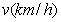 的函数。
的函数。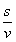 ,全程的运输成本为:
,全程的运输成本为: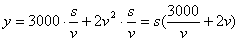 ………………………………..………………..….4分
………………………………..………………..….4分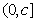 ……………………………………………….……………....….5分
……………………………………………….……………....….5分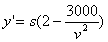 令
令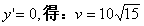 ………………….……………..….7分
………………….……………..….7分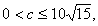
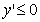 ,
,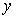 在
在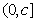 上递减,………….………………………….…..9分
上递减,………….………………………….…..9分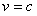 ,
,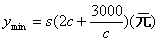 ………….……………………..…………………. .10分
………….……………………..…………………. .10分 当
当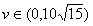 ,
,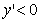
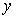 在
在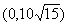 上递减;当
上递减;当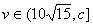 ,
,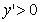 ,
,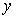 在
在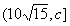 上递增………….………………………………………………………. 12分
上递增………….………………………………………………………. 12分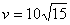 ,
,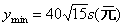 ………………………………………….………. 13分
………………………………………….………. 13分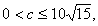 汽车行驶速度为c,最小运输成本是
汽车行驶速度为c,最小运输成本是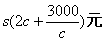 ;当
;当 汽车行驶速度为
汽车行驶速度为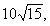 ,最小运输成本是
,最小运输成本是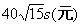 ;
;

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
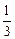 ),f(
),f(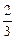 ),f(1)的大小关系_________.
),f(1)的大小关系_________. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
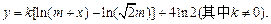 当燃料重量为
当燃料重量为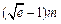 吨(e为自然对数的底数,
吨(e为自然对数的底数,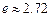 )时,该火箭的最大速度为4(km/s).(Ⅰ)求火箭的最大速度
)时,该火箭的最大速度为4(km/s).(Ⅰ)求火箭的最大速度 与燃料重量x吨之间的函数关系式
与燃料重量x吨之间的函数关系式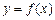 ;(Ⅱ)已知该火箭的起飞重量是544吨,是应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的轨道?
;(Ⅱ)已知该火箭的起飞重量是544吨,是应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的轨道?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com