
已知函数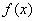 的定义域为
的定义域为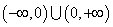 ,且满足条件:①
,且满足条件:①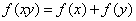 ;②
;②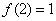 ;③当
;③当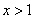 时,
时, .(1)求证:
.(1)求证: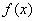 为偶函数;(2)讨论函数的单调性;(3)求不等式
为偶函数;(2)讨论函数的单调性;(3)求不等式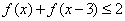 的解集.
的解集.
(1)证明:令x=y=1 有f(1)=f(1)+f(1) ∴f(1)=0
令x=y=-1 有f(1)=f(-1)+f(-1) ∴f(-1)=0
令y=-1 有f(-x)=f(x)+f(-1) ∴f(x)=f(-x)且定义域关于原式对称
∴f(x)是偶函数 法二:f(x2)=f(x)+f(x)
=f(-x)+f(-x)
∴f(x)=f(-x)
法三:令y=-1
f(-x)=f(x)+f(-1) ①
x=-x y=-1 f(x)=f(-x)+f(-1) ②
①-②
∴f(x)=f(-x)
(2)任取x1,x2∈(0,+ ∞)且x1<x2,则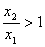
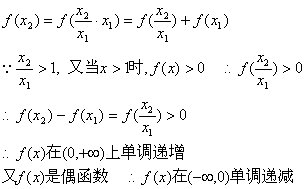
(3)
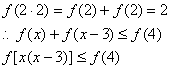
∵f(x)是偶函数
∴f(|x(x-3)|) ≤f(4)
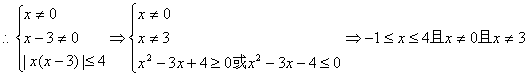
∴解集为[-1,0)∪(0,3)∪(3,4]


 优生乐园系列答案
优生乐园系列答案科目:高中数学 来源: 题型:
设点A(1,2)、B(-2,3),若直线ax+y+1=0与线段AB有交点,则a的取值范围是 ( )
A.[-3,2] B.[-2,3] C.(-∞,-2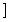 ∪[3,+∞) D.(-∞,-3
∪[3,+∞) D.(-∞,-3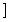 ∪[2,+∞)
∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知向量a=(sin θ,cos θ),其中θ∈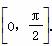 .
.
(1)若b=(2,1),a∥b,求sin θ和cos θ的值;
(2)若c=(-1,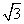 ),求|a+c|的最大值.
),求|a+c|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com