
【题目】已知函数f(x)=log2(|x﹣1|+|x+2|﹣a).
(Ⅰ)当a=7时,求函数f(x)的定义域;
(Ⅱ)若关于x的不等式f(x)≥3的解集是R,求实数a的取值范围.
【答案】解:(Ⅰ)由题设知:|x﹣1|+|x+2|>7,
令x﹣1=0,x+2=0,解得x=1,x=﹣2,这就是两个分界点.把全体实数分成3个区间.
不等式的解集是以下不等式组解集的并集:
![]() ,或
,或 ![]() ,或
,或 ![]()
解得函数f(x)的定义域为(﹣∞,﹣4)∪(3,+∞);
(Ⅱ)不等式f(x)≥3即:|x﹣1|+|x+2|≥a+8,
∵x∈R时,恒有|x﹣1|+|x+2|≥|(x﹣1)﹣(x+2)|=3,
∵不等式|x﹣1|+|x+2|≥a+8解集是R,∴a+8≤3,
∴a的取值范围是:(﹣∞,﹣5].
【解析】(1)根据零点分界讨论,脱掉绝对值,解出函数的定义域,(2)不等式f(x)≥3即:|x﹣1|+|x+2|≥a+8,根据绝对值不等式|a|+|b|≥|a﹣b|,解出a的取值范围.
【考点精析】本题主要考查了函数的定义域及其求法的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】对于无穷数列{an},记T={x|x=aj﹣ai , i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*且m>k),必有am+1﹣ak+1=t”,则称数列{an}具有性质P(t). (Ⅰ)若数列{an}满足 ![]() 判断数列{an}是否具有性质P(2)?是否具有性质P(4)?
判断数列{an}是否具有性质P(2)?是否具有性质P(4)?
(Ⅱ)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(Ⅲ)已知{an}是各项为正整数的数列,且{an}既具有性质P(2),又具有性质P(5),求证:存在整数N,使得aN , aN+1 , aN+2 , …,aN+k , …是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣x﹣1)ex .
(1)求函数f(x)的单调区间.
(2)若方程a( ![]() +1)+ex=ex在(0,1)内有解,求实数a的取值范围.
+1)+ex=ex在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,底面ABCD为边长为 ![]() 的正方形,PA⊥BD.
的正方形,PA⊥BD.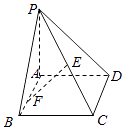
(1)求证:PB=PD;
(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣2,2]上的奇函数,当x∈(0,2]时,f(x)=2x﹣1,函数g(x)=x2﹣2x+m.如果对于x1∈[﹣2,2],x2∈[﹣2,2],使得g(x2)=f(x1),则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知总体的各个体的值由小到大依次为2,3,3,7,a,b,12,13.7,18.3,20,且总体的中位数为10.5,平均数为10.若要使该总体的方差最小,则a、b的取值分别是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com