
已知椭圆![]() 的离心率
的离心率![]() .
.
(Ⅰ)若椭圆准线间的距离为![]() ,求椭圆方程;
,求椭圆方程;
(Ⅱ)直线![]() 过点C(
过点C(![]() 交椭圆于A、B两点,且满足:
交椭圆于A、B两点,且满足:![]() ,试求
,试求![]() 面积的最大值.
面积的最大值.
解:(Ⅰ)∵椭圆的方程为![]() (a>b>0)
(a>b>0)
由e=![]() ,及a2=b2+c2,得a2=3b2
,及a2=b2+c2,得a2=3b2
又由准线间的距离为![]() ,得2
,得2![]()
∴a2=3,b2=1 ∴椭圆方程为![]() .
.
(Ⅱ)由e=![]() ,及a2=b2+c2,得a2=3b2, 可设椭圆的方程为
,及a2=b2+c2,得a2=3b2, 可设椭圆的方程为![]()
设A(x1,y1) , B(x2,y2) 由题知直线![]() 的斜率存在,则设
的斜率存在,则设![]() 的方程为y=k(x+1),
的方程为y=k(x+1),
由![]()
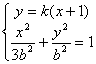
得:(3k2+1)x2+6k2x+3k2-3b2=0
且Δ=12(3b2-1)k2+12b2
∵直线![]() 交椭圆于两点,且
交椭圆于两点,且![]() ∴点C在椭圆内部,∴a>1
∴点C在椭圆内部,∴a>1
∴3b2>1 ∴Δ>0
∴x1+x2=![]()
∵![]() ∴(x1+1,y1)=3(-1-x2,-y2) ∴x1=-4-3x2
∴(x1+1,y1)=3(-1-x2,-y2) ∴x1=-4-3x2
∴x2+1=![]() ∴|x1-x2|=
∴|x1-x2|=![]()
又O到直线![]() 的距离为d=
的距离为d=![]()
∴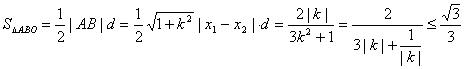
∴当且仅当3|k|=![]() ,即
,即![]() 时,
时,![]() 取最大值
取最大值![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在由圆O:x2+y2=1和椭圆C:
如图,在由圆O:x2+y2=1和椭圆C:| x2 |
| a2 |
| ||
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OM |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A,B是椭圆C:
如图,A,B是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com