
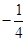 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;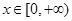 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;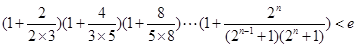 (其中
(其中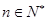 ,e是自然数对数的底数)
,e是自然数对数的底数)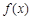 的单调递增区间为
的单调递增区间为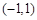 ,单调递减区间为
,单调递减区间为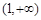 (2)
(2)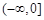 (3)见解析
(3)见解析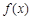 图象上的点都在
图象上的点都在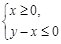 所表示的平面区域内,则当
所表示的平面区域内,则当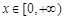 时,
时,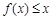 恒成立即可,即转化了恒成立问题,则只需要
恒成立即可,即转化了恒成立问题,则只需要 ,故考虑对
,故考虑对 求导求单调性来确定函数在
求导求单调性来确定函数在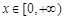 上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定
上的最大值,因为导函数含有参数a,所以在求解单调性确定最值的过程中需要讨论a的范围,讨论需从两根的大小和0的大小进行分析才能确定 的最值,从而得到a的取值范围.
的最值,从而得到a的取值范围.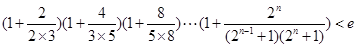 同时去对数再证明,即证明
同时去对数再证明,即证明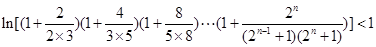 ,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)
,利用对数的乘法公式可以把不等式的左边化解成为不可求和数列的和,在利用利用(2)得到当a=0时,ln(1+x)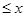 是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用
是恒成立的,把不可求和数列放缩成为可以裂项求和的数列,裂项利用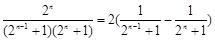 ,进而证明原不等式.
,进而证明原不等式. 时,
时,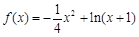 (
(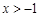 ),
),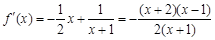 (
(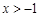 ), 1分
), 1分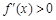 解得
解得 ,由
,由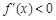 解得
解得 .
.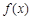 的单调递增区间为
的单调递增区间为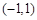 ,单调递减区间为
,单调递减区间为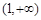 . 3分
. 3分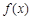 图象上的点都在
图象上的点都在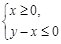 所表示的平面区域内,则当
所表示的平面区域内,则当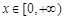 时,
时,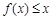 恒成立,即
恒成立,即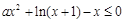 恒成立,
恒成立,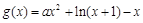 (
(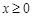 ),只需
),只需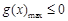 即可. 4分
即可. 4分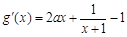
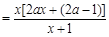 ,
,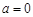 时,
时,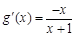 ,当
,当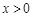 时,
时,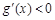 ,
,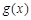 在
在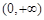 上单调递减,故
上单调递减,故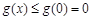 成立. 5分
成立. 5分 时,由
时,由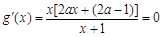 ,因
,因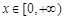 ,所以
,所以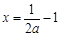 ,
,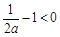 ,即
,即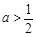 时,在区间
时,在区间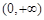 上,
上,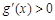 ,则函数
,则函数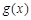 在
在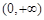 上单调递增,
上单调递增,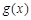 在
在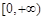 上无最大值(或:当
上无最大值(或:当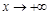 时,
时,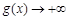 ),此时不满足条件;
),此时不满足条件;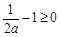 ,即
,即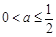 时,函数
时,函数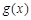 在
在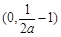 上单调递减,
上单调递减,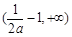 上单调递增,同样
上单调递增,同样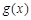 在
在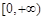 上无最大值,不满足条件. 8分
上无最大值,不满足条件. 8分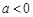 时,由
时,由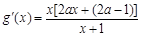 ,∵
,∵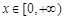 ,∴
,∴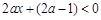 ,
,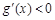 ,故函数
,故函数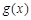 在
在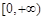 上单调递减,故
上单调递减,故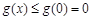 成立.
成立.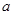 的取值范围是
的取值范围是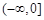 . 10分
. 10分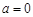 时,
时,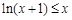 在
在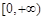 上恒成立.
上恒成立.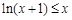 在区间
在区间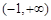 上恒成立), 11分
上恒成立), 11分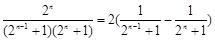 ,
,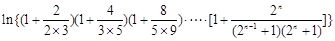
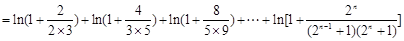
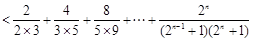
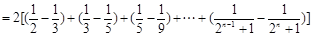
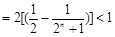 ,
,
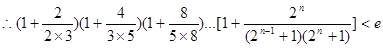 . 14分
. 14分

科目:高中数学 来源:不详 题型:解答题
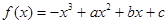 在
在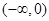 上是减函数,在
上是减函数,在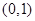 上是增函数,函数
上是增函数,函数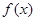 在
在 上有三个零点,且
上有三个零点,且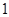 是其中一个零点.
是其中一个零点.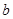 的值;
的值;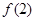 的取值范围;
的取值范围;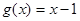 ,且
,且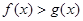 的解集为
的解集为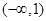 ,求实数
,求实数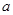 的取值范围.
的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com