
分析 (1)根据函数f(x)的解析式,分别计算f($\frac{3}{2}$)以及f(f($\frac{1}{2}$))的值即可;
(2)分别解出关于x<$\frac{1}{2}$和x≥$\frac{1}{2}$时的不等式的解集取并集即可.
解答 解:(1)f($\frac{3}{2}$)=${log}_{\frac{1}{2}}$(2×$\frac{3}{2}$+1)=${log}_{\frac{1}{2}}$4=$\frac{{log}_{2}4}{{log}_{2}\frac{1}{2}}$=-2,
f($\frac{1}{2}$)=${log}_{\frac{1}{2}}$(2×$\frac{1}{2}$+1)=${log}_{\frac{1}{2}}$2=-1,
故f(f($\frac{1}{2}$))=f(-1)=(-1)2-4×(-1)=5;
(2)x<$\frac{1}{2}$时,x2-4x>-3,解得:x<1,或x>3(舍),
故x<$\frac{1}{2}$成立,
x≥$\frac{1}{2}$时,${log}_{\frac{1}{2}}$(2x+1)>-3,
故2x+1<8,解得:x<$\frac{7}{2}$,
综上,不等式的解集是:$\left\{{x\left|{x<\frac{7}{2}}\right.}\right\}$.
点评 本题考查了函数求值问题,考查解不等式问题,是一道基础题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.
已知P是圆C:(x+1)2+y2=16.上任意一点,A(1,0),线段PA的垂直平分线与PC相交于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
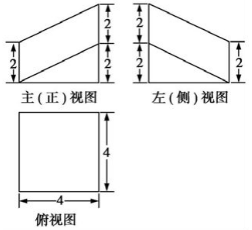
| A. | 32+8$\sqrt{6}$ | B. | 48+8$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 44+8$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $-\frac{1}{3}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com