
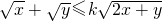 对于任意正实数x,y成立,求k的取值范围.
对于任意正实数x,y成立,求k的取值范围. +
+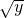 )2≤k2(2x+y)?(2k2-1)x-2
)2≤k2(2x+y)?(2k2-1)x-2 +(k2-1)y≥0对于x,y>0恒成立.两边同除以y得(2k2-1)
+(k2-1)y≥0对于x,y>0恒成立.两边同除以y得(2k2-1) -2
-2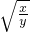 +(k2-1)≥0
+(k2-1)≥0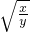 >0,则得f(t)=(2k2-1)t2-2t+(k2-1)≥0对一切t>0恒成立.
>0,则得f(t)=(2k2-1)t2-2t+(k2-1)≥0对一切t>0恒成立. 时,f(t)取得最小值
时,f(t)取得最小值 -
-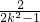 +k2-1=
+k2-1= =
= .
. 时,不等式恒成立,且当x=4y>0时等号成立.
时,不等式恒成立,且当x=4y>0时等号成立. ,+∞).
,+∞).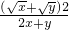 =
= ,令t=
,令t=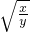 >0,,则k2≥
>0,,则k2≥ =
= (1+
(1+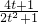 ).2t2+1
).2t2+1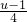 ,
,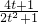 =
= 只要求s(u)=
只要求s(u)= 的最大值.
的最大值.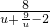 ≤
≤ =2,于是
=2,于是 (1+
(1+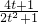 )≤
)≤ (1+2)=
(1+2)= .
. ,即k≥
,即k≥ 时,不等式恒成立(当x=4y>0时等号成立).
时,不等式恒成立(当x=4y>0时等号成立).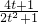 ,则s′(t)=
,则s′(t)= =
=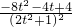 ,t>0时有驻点t=
,t>0时有驻点t= .且在0<t<
.且在0<t< 时,s′(t)>0,在t>
时,s′(t)>0,在t> 时,s′(t)<0,即s(t)在t=
时,s′(t)<0,即s(t)在t= 时取得最大值2,此时有k2≥
时取得最大值2,此时有k2≥ (1+s(
(1+s( ))=
))= .
. +
+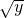 )2≤(
)2≤( +1)(2x+y).
+1)(2x+y). +
+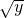 )≤
)≤
 对一切正实数x,y成立.
对一切正实数x,y成立. 时,取x=
时,取x= ,y=1,有
,y=1,有 +
+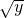 =
= ,而k
,而k =k
=k <
< ×
× =
= .即不等式不能恒成立.
.即不等式不能恒成立. 时,由于对一切正实数x,y,都有
时,由于对一切正实数x,y,都有 +
+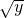 ≤
≤
 ≤k
≤k ,故不等式恒成立.
,故不等式恒成立. ,+∞).
,+∞). +(k2-1)y≥0对于x,y>0恒成立.两边同除以y得(2k2-1)
+(k2-1)y≥0对于x,y>0恒成立.两边同除以y得(2k2-1) -2
-2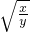 +(k2-1)≥0,令t=
+(k2-1)≥0,令t=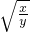 >0,构造得出f(t)=(2k2-1)t2-2t+(k2-1)≥0对一切t>0恒成立.利用二次函数的性质求解.
>0,构造得出f(t)=(2k2-1)t2-2t+(k2-1)≥0对一切t>0恒成立.利用二次函数的性质求解.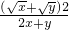 =
= ,令t=
,令t=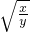 >0,,则k2≥
>0,,则k2≥ =
= (1+
(1+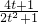 ).只需求出
).只需求出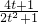 的最大值即可,可以利用基本不等式或导数法求出.
的最大值即可,可以利用基本不等式或导数法求出. +
+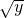 )2≤(
)2≤( +1)(2x+y).即(
+1)(2x+y).即( +
+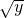 )≤
)≤
 对一切正实数x,y成立.分k<
对一切正实数x,y成立.分k< ,k≥
,k≥ 两种情况讨论.
两种情况讨论.

科目:高中数学 来源: 题型:
| x2+ax+2 |
| 1 |
| 3 |
| 11 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012届度湖南省高三下学期二轮复习理科数学试卷 题型:解答题
已知函数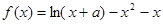 在点
在点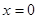 处取得极值。
处取得极值。
(1)求实数a的值;
(2)若关于x的方程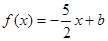 在区间[0,2]上有两个不等实根,求b的取值范围;
在区间[0,2]上有两个不等实根,求b的取值范围;
(3)证明:对于任意的正整数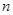 ,不等式
,不等式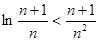 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
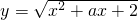 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2]; 对称.
对称.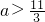 ;
;查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知函数![]() 在点
在点![]() 处取得极值.
处取得极值.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等实根,求
上有两个不等实根,求![]() 的取值范围;
的取值范围;
(Ⅲ)证明:对于任意的正整数![]() ,不等式
,不等式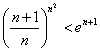 都成立.
都成立.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷3(文科)(解析版) 题型:解答题
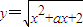 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];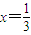 对称.
对称.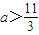 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com