
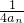 ,其中n∈N*.
,其中n∈N*.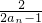 ,求证:数列{bn}是等差数列,并求出{an}的通项公式an;
,求证:数列{bn}是等差数列,并求出{an}的通项公式an;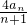 ,数列{CnCn+2}的前n项和为Tn,是否存在正整数m,使得Tn<
,数列{CnCn+2}的前n项和为Tn,是否存在正整数m,使得Tn<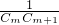 对于n∈N*恒成立,若存在,求出m的最小值,若不存在,请说明理由.
对于n∈N*恒成立,若存在,求出m的最小值,若不存在,请说明理由. =
=
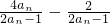 =2,
=2,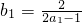 =2,∴bn=2+(n-1)×2=2n.
=2,∴bn=2+(n-1)×2=2n.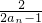 ,解得
,解得 .
.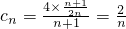 ,
,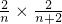 =
=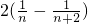 ,
,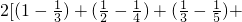 …
…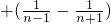 +
+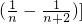
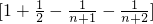 <3.
<3.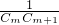 对于n∈N*恒成立,只要
对于n∈N*恒成立,只要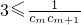 ,即
,即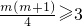 ,
,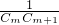 对于n∈N*恒成立,只要
对于n∈N*恒成立,只要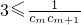 ,即
,即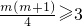 ,解出即可.
,解出即可.

科目:高中数学 来源: 题型:
| 3+4an |
| 12-4an |
| 1 | ||
an-
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2 |
| 3nan-1 |
| 2an-1+n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com