
【题目】将函数f(x)= ![]() sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移
sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移 ![]() 个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:f(x)= ![]() sinxcosx+sin2x=
sinxcosx+sin2x= ![]() sin2x﹣
sin2x﹣ ![]() cos2x+
cos2x+ ![]() =sin(2x﹣
=sin(2x﹣ ![]() )+
)+ ![]() , 图象上各点的纵坐标不变,横坐标变为原来的2倍,可得对应的函数解析式为y=sin(x﹣
, 图象上各点的纵坐标不变,横坐标变为原来的2倍,可得对应的函数解析式为y=sin(x﹣ ![]() )+
)+ ![]() ,
,
再沿x轴向右平移 ![]() 个单位,得到函数解析式为y=g(x)=sin(x﹣
个单位,得到函数解析式为y=g(x)=sin(x﹣ ![]() ﹣
﹣ ![]() )+
)+ ![]() =sin(x﹣
=sin(x﹣ ![]() )+
)+ ![]() ,
,
令x﹣ ![]() ∈[2kπ﹣
∈[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈Z,解得:x∈[﹣
],k∈Z,解得:x∈[﹣ ![]() +2kπ,kπ+
+2kπ,kπ+ ![]() ],k∈Z,
],k∈Z,
取k=0,可得:x∈[﹣ ![]() ,
, ![]() ].
].
故选:A.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】袋中装有偶数个球,其中红球、黑球各占一半.甲、乙、丙是三个空盒.每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒.重复上述过程,直到袋中所有球都被放入盒中,则( )
A.乙盒中黑球不多于丙盒中黑球
B.乙盒中红球与丙盒中黑球一样多
C.乙盒中红球不多于丙盒中红球
D.乙盒中黑球与丙盒中红球一样多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣φ)﹣ ![]() sin(2x﹣φ)(|φ|<
sin(2x﹣φ)(|φ|< ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位后关于y轴对称,则f(x)在区间
个单位后关于y轴对称,则f(x)在区间 ![]() 上的最小值为( )
上的最小值为( )
A.﹣1
B.![]()
C.![]()
D.﹣2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
ax3﹣bex(a∈R,b∈R),且f(x)在x=0处的切线与x﹣y+3=0垂直.
(1)若函数f(x)在[ ![]() ,1]存在单调递增区间,求实数a的取值范围;
,1]存在单调递增区间,求实数a的取值范围;
(2)若f′(x)有两个极值点x1 , x2 , 且x1<x2 , 求a的取值范围;
(3)在第二问的前提下,证明:﹣ ![]() <f′(x1)<﹣1.
<f′(x1)<﹣1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD= ![]() BC=2,E在BC上,且BE=
BC=2,E在BC上,且BE= ![]() AB=1,侧棱PA⊥平面ABCD.
AB=1,侧棱PA⊥平面ABCD. 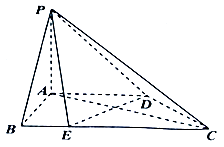
(1)求证:平面PDE⊥平面PAC;
(2)若△PAB为等腰直角三角形. (i)求直线PE与平面PAC所成角的正弦值;
(ii)求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=2时,求不等式f(x)<g(x)的解集;
(2)设a> ![]() ,且当x∈[
,且当x∈[ ![]() ,a]时,f(x)≤g(x),求a的取值范围.
,a]时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD= ![]() CD=1.
CD=1. 
(1)若M为PA中点,求证:AC∥平面MDE;
(2)若平面PAD与PBC所成的锐二面角的大小为 ![]() ,求线段PD的长度.
,求线段PD的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com