
分析 (1)利用导数的几何意义即可得出;
(2)通过求导得到g′(x),即可得出其单调性;
(3)利用斜率计算公式,利用分析法即可证明.
解答 解:(1)依题意得g(x)=lnx+ax2+bx,则g′(x)=$\frac{1}{x}$+2ax+b.
由函数g(x)的函数图象在点(1,g(1))处的切线平行于x轴得:g′(1)=1+2a+b=0,
∴b=-2a-1 …(4分)
(2)由(1)得g′(x)=$\frac{2a{x}^{2}-(2a+1)x+1}{x}$(x>0)
∵函数g(x)的定义域为(0,+∞).
∵a≤0,f′(x)≤0,函数g(x)的单调减区间为(0,+∞).…(10分)
(3)依题意得k=$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$,
证$\frac{1}{x_2}$<k<$\frac{1}{x_1}$,即证$\frac{1}{x_2}$<$\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}$<$\frac{1}{x_1}$
因x2-x1>0,即证$\frac{{x}_{2}-{x}_{1}}{{x}_{2}}$<ln$\frac{{x}_{2}}{{x}_{1}}$<$\frac{{x}_{2}-{x}_{1}}{{x}_{1}}$.
令$\frac{{x}_{2}}{{x}_{1}}$=t(t>1),即证1-$\frac{1}{t}$<lnt<t-1(t>1)
令h(t)=lnt+$\frac{1}{t}$-1(t>1)则h′(t)=$\frac{t-1}{{t}^{2}}$>0
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即lnt>1-$\frac{1}{t}$(t>1)①
同理可证:lnt<t-1②
综①②得1-$\frac{1}{t}$<lnt<t-1(t>1),即$\frac{1}{x_2}$<k<$\frac{1}{x_1}$. …(16分)
点评 熟练掌握利用导数研究函数的单调性、导数的几何意义,考查分析法的运用,根据所证明的结论恰当的构造函数是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 120° | C. | 60°或120° | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
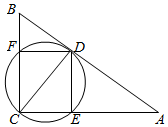 如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.
如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或0<x<1} | D. | {x|x<-1或x>1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在R上单调递增 | B. | f(x)在R上是常数 | C. | f(x)在R上不单调 | D. | f(x)在R上单调递减 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com