
A.60° B.90° C.105° D.75°
解析一:设AB、BB1、B![]()
![]() AB1, HF
AB1, HF![]()
![]() C1B,
C1B,
则∠PHF即为异面直线AB1与C1B所成的角.
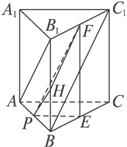
连结PF,并设BB1=1,则正三棱柱的底面边长为![]() ,不难求得PH=HF=
,不难求得PH=HF=![]() .
.
取BC的中点E,连结PE、EF,易知△PEF是直角三角形,在Rt△PEF中, PF2=![]() ,显然有PH2+HF2=PF2.
,显然有PH2+HF2=PF2.
故∠PHF=90°.故选B.
解析二:如图,延长AB到D,使BD=AB,作DD1![]() AA1,连结B1D1、BD1.
AA1,连结B1D1、BD1.
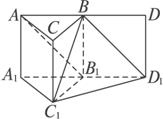
∵AB![]() B1D1,
B1D1,
∴AB1![]() BD1.
BD1.
故∠C1BD1即为所求异面直线所成的角.
易求得BC1=BD1=![]() ,C1D1=2×
,C1D1=2×![]() ×sin60°=
×sin60°=![]() .
.
又∵BC12+BD12=C1D12,
∴∠C1BD1=90°.
故选B.
解析三:设法把BC1的B点平移到B1处,为使平移后的位置确定且易于计算,可在已知三棱柱的下面作一个同样的三棱柱.
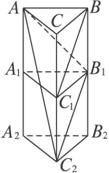
作直三棱柱A1B
∵BB![]()
∴C1B![]() C2B1,则∠AB
C2B1,则∠AB
易求得∠AB
答案:B


科目:高中数学 来源: 题型:
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
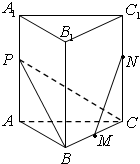 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且PA=
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且PA=
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源:2011年四川省绵阳中学高考适应性检测数学试卷(理科)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com