练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数，则满足的x的取值范围是(    )

    A．，2]       B．[0，2]         C．[1，+)       D．[0，+)


    D


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示，四棱锥的底面是正方形，每条侧棱长都是底面边长的倍，为侧棱上的点.

    (1)求证：；

    (2)若平面，则侧棱上是否存在一点，使得平面.

    若存在，求的值；若不存在，试说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某制造商3月生产了一批乒乓球，随机抽样100个进行检查，测得每个球的直径(单位：mm)，将数据分组如下：

    分组

    频数

    频率

    [39.95,39.97)

    10

    [39.97,39.99)

    20

    [39.99,40.01)

    50

    [40.01,40.03]

    20

    合计

    100

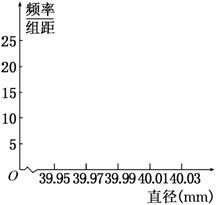
    (1)请在上表中补充完成频率分布表(结果保留两位小数)，并在图中画出频率分布直方图；

    (2)若以上述频率作为概率，已知标准乒乓球的直径为40.00 mm，试求这批球的直径误差不超过0.03 mm的概率；

    (3)统计方法中，同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00)作为代表．据此估计这批乒乓球直径的平均值(结果保留两位小数)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则          

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义非零向量的“相伴函数”为，向量称为的“相伴向量”（其中O为坐标原点）．记平面内所有向量的“相伴函数”构成的集合为

    （1）设

    ①求证：

    ②求（1）中函数h（x）的“相伴向量”的模；

    （2）已知点满足：，向量“相伴函数”在处取得最大值，求的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于集合M、N，定义M－N＝{x|x∈M且x∉N}，M⊕N＝(M－N)∪(N－M)，设A＝{y|y＝3x， x∈R}，B＝{y|y＝－(x－1)2＋2，x∈R}，则A⊕B等于(　　)

    A．[0,2)                 B．(0,2]

    C．(－∞，0]∪(2，＋∞)  D．(－∞，0)∪[2，＋∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列结论中是真命题的是__________(填序号)．

    ①f(x)＝ax2＋bx＋c在[0，＋∞)上是增函数的一个充分条件是－＜0；

    ②已知甲：x＋y≠3，乙：x≠1或y≠2，则甲是乙的充分不必要条件；

    ③数列{an}(n∈N*)是等差数列的充要条件是Pn是共线的．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    四位学生，坐在一排有7个位置的座位上，有且只有两个空位是相邻的不同坐法有________种．(用数字作答)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设数列{an}的前n项和为Sn­，若 是一个定值，则下各数中也为定值                                      （   ）

    A                         B               C            D 

    查看答案和解析>>

    同步练习册答案