
【题目】已知m、n、s、t∈R* , m+n=3, ![]() 其中m、n是常数且m<n,若s+t的最小值 是
其中m、n是常数且m<n,若s+t的最小值 是 ![]() ,满足条件的点(m,n)是椭圆
,满足条件的点(m,n)是椭圆 ![]() 一弦的中点,则此弦所在的直线方程为( )
一弦的中点,则此弦所在的直线方程为( )
A.x﹣2y+3=0
B.4x﹣2y﹣3=0
C.x+y﹣3=0
D.2x+y﹣4=0
【答案】D
【解析】解:∵sm、n、s、t为正数,m+n=3, ![]() ,s+t的最小值 是
,s+t的最小值 是 ![]() , ∴(s+t)(
, ∴(s+t)( ![]() )的最小值 是
)的最小值 是 ![]() ,
,
∴(s+t)( ![]() )=m+n+
)=m+n+ ![]()
![]() ,满足
,满足 ![]() 时取最小值,
时取最小值,
此时最小值为m+n+2 ![]() =3+2
=3+2 ![]() ,得:mn=2,又:m+n=3,所以,m=1,n=2.
,得:mn=2,又:m+n=3,所以,m=1,n=2.
设以(1,2)为中点的弦交椭圆椭圆 ![]() 于A(x1 , y1),B(x2 , y2),
于A(x1 , y1),B(x2 , y2),
由中点从坐标公式知x1+x2=2,y1+y2=4,
把A(x1 , y1),B(x2 , y2)分别代入4x2+y2=16,
得 ![]()
两式相减得2(x1﹣x2)+(y1﹣y2)=0,
∴k= ![]() .∴此弦所在的直线方程为y﹣2=﹣2(x﹣1),
.∴此弦所在的直线方程为y﹣2=﹣2(x﹣1),
即2x+y﹣4=0.
故选:D.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中, ![]() 平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形,
平面PCD,平面PAD平面ABCD,CD⊥AD,△APD为等腰直角三角形, ![]() .
. 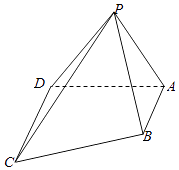
(1)证明:平面PAB⊥平面PCD;
(2)若三棱锥B﹣PAD的体积为 ![]() ,求平面PAD与平面PBC所成二面角的余弦值.
,求平面PAD与平面PBC所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列几个式子,结果为 ![]() 的序号是 . ①tan25°+tan35°
的序号是 . ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,其中a>0,a≠1.
,其中a>0,a≠1.
(Ⅰ)若f(x)在(﹣∞,+∞)上是单调函数,求实数a,b的取值范围;
(Ⅱ)当a=2时,函数f(x)在(﹣∞,+∞)上只有一个零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的三个顶点分别为A(0,4)、B(-2,6)、C(-8,0).
(1)分别求边AC和AB所在直线的方程;
(2)求AC边上的中线BD所在直线的方程;
(3)求AC边的中垂线所在直线的方程;
(4)求AC边上的高所在直线的方程;
(5)求经过两边AB和AC的中点的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前项n和为Sn , 若对于任意的正整数n都有Sn=2an﹣3n.
(1)设bn=an+3,求证:数列{bn}是等比数列,并求出{an}的通项公式.
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC , AE⊥DC , M , N分别是AD , BE的中点,将三角形ADE沿AE折起,则下列说法正确的是(填序号).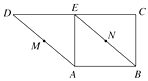
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,设函数
,设函数 ![]() .
.
(1)求函数 ![]() 的单调递增区间;
的单调递增区间;
(2)在 ![]() 中,边
中,边 ![]() 分别是角
分别是角 ![]() 的对边,角
的对边,角 ![]() 为锐角,若
为锐角,若![]() ,
, ![]() ,
, ![]() 的面积为
的面积为 ![]() ,求边
,求边 ![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com