练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    因为a，b∈R+，a+b≥2
    		ab
    ，…大前提
    x+
    1
    x
    ≥2
    		x•
    1
    x
    ，…小前提
    所以x+
    1
    x
    ≥2，…结论
    以上推理过程中的错误为（　　）
    A、小前提B、大前提
    C、结论D、无错误
    分析：演绎推理是由一般到特殊的推理，是一种必然性的推理，演绎推理得到的结论不一定是正确的，这要取决与前提是否真实和推理的形式是否正确，演绎推理一般模式是“三段论”形式，即大前提小前提和结论．
    解答：解：∵a，b∈R+，a+b≥2
    		ab
    ，
    这是基本不等式的形式，注意到基本不等式的使用条件，a，b都是正数，
    x+
    1
    x
    ≥2
    		x•
    1
    x
    是小前提，没有写出x的取值范围，
    ∴本题中的小前提有错误，
    故选A．
    点评：本题考查演绎推理的意义，演绎推理是由一般性的结论推出特殊性命题的一种推理模式，演绎推理的前提与结论之间有一种蕴含关系．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列推理合理的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列推理合理的是（　　）
    A、f（x）是增函数，则f′（x）＞0B、因为a＞b（a，b∈R），则a+2i＞b+2iC、△ABC为锐角三角形，则sinA+sinB＞cosA+cosBD、直线l1∥l2，则k1=k2

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省潮州市金山中学高二（下）4月模块数学试卷（理科）（解析版） 题型：选择题

    下列推理合理的是（ ）
    A．f（x）是增函数，则f'（x）＞0
    B．因为a＞b（a、b∈R），所以a+2i＞b+2i（i是虚数单位）
    C．α、β是锐角△ABC的两个内角，则sinα＞cosβ
    D．直线l1∥l2，则k1=k2（k1、k2分别为直线l1、l2的斜率）

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试理科数学（北京卷解析版） 题型：解答题

    已知曲线C:(m∈R)

    （1）   若曲线C是焦点在x轴点上的椭圆，求m的取值范围；

    （2）     设m=4，曲线c与y轴的交点为A，B（点A位于点B的上方），直线y=kx+4与曲线c交于不同的两点M、N,直线y=1与直线BM交于点G.求证：A，G，N三点共线。

    【解析】（1）曲线C是焦点在x轴上的椭圆，当且仅当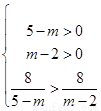解得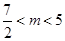，所以m的取值范围是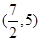

    (2)当m=4时，曲线C的方程为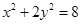，点A,B的坐标分别为，

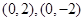    由，得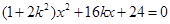

    因为直线与曲线C交于不同的两点，所以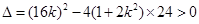

    即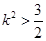

    设点M，N的坐标分别为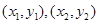，则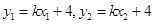

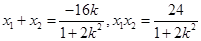
    直线BM的方程为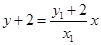，点G的坐标为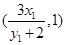

    因为直线AN和直线AG的斜率分别为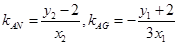

    所以

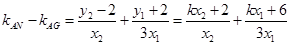
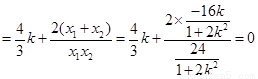
    即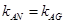,故A，G，N三点共线。

     

    查看答案和解析>>

    同步练习册答案