
【题目】在△ABC中, ![]() .
.
(Ⅰ)若c2=5a2+ab,求 ![]() ;
;
(Ⅱ)求sinAsinB的最大值.
【答案】解:(Ⅰ)由余弦定理可得:c2=a2+b2﹣2abcosC=a2+b2+ab,
又由c2=5a2+ab,则有5a2+ab=a2+b2+ab,
变形可得b2=4a2 , 即b=2a,
则 ![]() =
= ![]() =2;
=2;
(Ⅱ)根据题意, ![]() ,则A+B=
,则A+B= ![]() ,即B=
,即B= ![]() ﹣A,
﹣A,
sinAsinB=sinAsin( ![]() ﹣A)=sinA[
﹣A)=sinA[ ![]() cosA﹣
cosA﹣ ![]() sinA]
sinA]
= ![]() sinAcosA﹣
sinAcosA﹣ ![]() sin2A=
sin2A= ![]() ﹣
﹣ ![]()
= ![]() ﹣
﹣ ![]() ,
,
又由A+B= ![]() ,则0<A<
,则0<A< ![]() ,
,
则 ![]() <2A+
<2A+ ![]() <
< ![]() ,
,
进而有0< ![]() ﹣
﹣ ![]() ≤
≤ ![]() ,
,
即0<sinAsinB≤ ![]() ,
,
故sinAsinB的最大值为 ![]()
【解析】(Ⅰ)根据题意,结合余弦定理可得5a2+ab=a2+b2+ab,变形可得b2=4a2 , 即b=2a,由正弦定理分析可得答案;(Ⅱ)根据题意, ![]() ,可得B=
,可得B= ﹣A,将sinAsinB变形可得sinAsinB=
![]() ﹣
﹣ ![]() ,结合A的范围,分析可得
,结合A的范围,分析可得 ![]() ﹣
﹣ ![]() 即sinAsinB的范围,即可得答案.
即sinAsinB的范围,即可得答案.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C所对的边分别为a,b,c,且a2+b2﹣c2= ![]() ab.
ab.
(1)求cos ![]() 的值;
的值;
(2)若c=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=3sin(4x+ ![]() )图象上所有点的横坐标伸长到原来的2倍,再向右平移
)图象上所有点的横坐标伸长到原来的2倍,再向右平移 ![]() 个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
个单位长度,得到函数y=g(x)的图象,则y=g(x)图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A,B,C,D四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请A片区房源的概率;
(2)用x表示选择A片区的人数,求x的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来共享单车在我国主要城市发展迅速.目前市场上有多种类型的共享单车,有关部门对其中三种共享单车方式(M方式、Y方式、F方式)进行统计(统计对象年龄在15~55岁),相关数据如表1,表2所示. 三种共享单车方式人群年龄比例(表1)
方式 | M | Y | F |
[15,25) | 25% | 20% | 35% |
[25,35) | 50% | 55% | 25% |
[35,45) | 20% | 20% | 20% |
[45,55] | 5% | a% | 20% |
不同性别选择共享单车种类情况统计(表2)
性别 | 男 | 女 |
1 | 20% | 50% |
2 | 35% | 40% |
3 | 45% | 10% |
(Ⅰ)根据表1估算出使用Y共享单车方式人群的平均年龄;
(Ⅱ)若从统计对象中随机选取男女各一人,试估计男性使用共享单车种类数大于女性使用共享单车种类数的概率;
(Ⅲ)现有一个年龄在25~35岁之间的共享单车用户,那么他使用Y方式出行的概率最大,使用F方式出行的概率最小,试问此结论是否正确?(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,an},ai∈R,i=1,2,…,n,并且n≥2. 定义 ![]() (例如:
(例如: ![]() ).
).
(Ⅰ)若A={1,2,3,4,5,6,7,8,9,10},M={1,2,3,4,5},集合A的子集N满足:N≠M,且T(M)=T(N),求出一个符合条件的N;
(Ⅱ)对于任意给定的常数C以及给定的集合A={a1 , a2 , …,an},求证:存在集合B={b1 , b2 , …,bn},使得T(B)=T(A),且 ![]() .
.
(Ⅲ)已知集合A={a1 , a2 , …,a2m}满足:ai<ai+1 , i=1,2,…,2m﹣1,m≥2,a1=a,a2m=b,其中a,b∈R为给定的常数,求T(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等腰三角形ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使P﹣AE﹣C为120°,设点P在面ABE上的射影为H. 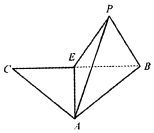
(1)证明:点H为EB的中点;
(2)若 ![]() ,求直线BE与平面ABP所成角的正弦值.
,求直线BE与平面ABP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在各项均为正数的等比数列{an}中,a1=2,且2a1 , a3 , 3a2成等差数列.
(Ⅰ) 求等比数列{an}的通项公式;
(Ⅱ) 若数列{bn}满足bn=11﹣2log2an , 求数列{bn}的前n项和Tn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|4≤2x<128},B={x|1<x≤6},M={x|a﹣3<x<a+3}.
(1)求A∩UB;
(2)若M∪UB=R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com