
【题目】函数![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 为偶函数,当
为偶函数,当![]() 时,
时,![]() ,若
,若![]() 有三个零点,则实数
有三个零点,则实数![]() 的取值集合是________.
的取值集合是________.
【答案】![]()
![]()
【解析】
先根据条件判断函数![]() 的对称性和周期性,再求出函数
的对称性和周期性,再求出函数![]() 在一个周期内的解析式;要求
在一个周期内的解析式;要求![]() 的零点问题,可令
的零点问题,可令![]() ,得
,得![]() ,然后在同一个坐标系中画出
,然后在同一个坐标系中画出![]() 和
和![]() 的图像,通过观察图像,列式求解得
的图像,通过观察图像,列式求解得![]() 的取值范围.
的取值范围.
因为![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() 的对称中心是
的对称中心是![]() 点,
点,
因为![]() 为偶函数,所以
为偶函数,所以![]() 的对称轴是
的对称轴是![]() ,所以
,所以![]() 的对称轴是
的对称轴是![]() ,
,
所以![]() 的周期
的周期![]() ,
,
且![]() 也是
也是![]() 的对称轴,
的对称轴,
因为![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,![]() 时,
时,![]() ,
,
所以![]() 时
时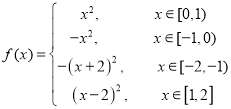 ,
,
因为![]() 有三个零点,
有三个零点,
所以令![]() ,得
,得![]() ,
,
即![]() 和
和![]() 的图像有三个不同的交点,
的图像有三个不同的交点,
因为在一个周期内,
当直线![]() 与
与![]() 在
在![]() 内相切时,令
内相切时,令![]() ,
,
得![]() ,
,![]() ,
,
所以![]() ,得
,得![]() ,
,
此时,![]() 在
在![]() 处得
处得![]() ,
,
即直线![]() 与
与![]() 在
在![]() 内没有交点,在
内没有交点,在![]() 内有两个交点,
内有两个交点,
所以要使![]() 和
和![]() 的图像有三个不同的交点,需
的图像有三个不同的交点,需![]() ,
,
当直线![]() 与
与![]() 在
在![]() 内相切时,令
内相切时,令![]() ,
,
得![]() ,
,![]() ,
,
所以![]() ,得
,得![]() ,
,
此时,![]() 在
在![]() 处得
处得![]() ,
,
即直线![]() 与
与![]() 在
在![]() 内没有交点,
内没有交点,![]() 在内有两个交点,
在内有两个交点,
所以要使![]() 和
和![]() 的图像有三个不同的交点,需
的图像有三个不同的交点,需![]() ,
,
综上![]() ,
,
所以,由周期性得![]()
![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究证实,二氧化碳等温室气体的排放(简称碳排放)对全球气候和生态环境产生了负面影响.环境部门对A市每年的碳排放总量规定不能超过550万吨,否则将采取紧急限排措施.已知A市2013年的碳排放总量为400万吨,通过技术改造和倡导低碳生活等措施,此后每年的碳排放量比上一年的碳排放总量减少10%.同时,因经济发展和人口增加等因素,每年又新增加碳排放量m万吨(m>0).
(1)求A市2015年的碳排放总量(用含m的式子表示);
(2)若A市永远不需要采取紧急限排措施,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”。在以下四个函数中:①
是“控制增长函数”。在以下四个函数中:①![]() ②
②![]() ③
③![]() ④
④![]() 是“控制增长函数”的有(空格上填入函数代码)________.
是“控制增长函数”的有(空格上填入函数代码)________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,C1的参数方程为 (t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(t为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,C2的极坐标方程ρ2-2ρcos θ-3=0.
(Ⅰ)说明C2是哪种曲线,并将C2的方程化为普通方程;
(Ⅱ)C1与C2有两个公共点A,B,定点P的极坐标![]() ,求线段AB的长及定点P到A,B两点的距离之积.
,求线段AB的长及定点P到A,B两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,给出下列四个命题:
,给出下列四个命题:
①若![]() 是偶函数,则
是偶函数,则![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
②若![]() ,则
,则![]() 的图像关于点
的图像关于点![]() 对称;
对称;
③若![]() ,且
,且![]() ,则
,则![]() 的一个周期为2;
的一个周期为2;
④![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称;
对称;
其中正确命题的序号为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com