Question

【题目】已知函数 ，a为正常数．
（1）若f（x）=lnx+φ（x），且 ，求函数f（x）的单调增区间；
（2）若g（x）=|lnx|+φ（x），且对任意x1 ， x2∈（0，2]，x1≠x2 ， 都有 ，求a的取值范围．

Answer 1

【答案】
（1）解： ，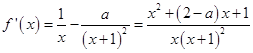

∵ ，令f′（x）＞0，得x＞2，或 ，

∴函数f（x）的单调增区间为 ，（2，+∞）

（2）解：∵ ，

∴ ，

∴ ，

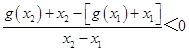设h（x）=g（x）+x，依题意，h（x）在（0，2]上是减函数．

当1≤x≤2时， ， ，

令h′（x）≤0，得： 对x∈[1，2]恒成立，

设 ，则 ，

∵1≤x≤2，∴ ，

∴m（x）在[1，2]上递增，则当x=2时，m（x）有最大值为 ，

∴

当0＜x＜1时， ， ，

令h′（x）≤0，得： ，

设 ，则 ，

∴t（x）在（0，1）上是增函数，

∴t（x）＜t（1）=0，

∴a≥0．

综上所述，

【解析】（1）先对函数y=f（x）进行求导，然后令导函数大于0（或小于0）求出x的范围，根据f′（x）＞0求得的区间是单调增区间，f′（x）＜0求得的区间是单调减区间，即可得到答案．（2）设h（x）=g（x）+x，依题意得出h（x）在（0，2]上是减函数．下面对x分类讨论：①当1≤x≤2时，②当0＜x＜1时，利用导数研究函数的单调性从及最值，即可求得求a的取值范围．