解:记顾客购买一件产品,获一等奖为事件A
1,获二等奖为事件A
2,不获奖为事件A
0,
则P(A
1)=0.1,P(A
2)=0.3,P(A
0)=0.6.
(1)该顾客购买2件产品,中奖的概率为
P=1-P(A
0•A
0)=1-[P(A
0)]
2=1-0.6
2=0.64.
(2)该顾客获得奖金数不小于100元的可能值为100元、120元、200元,
依次记这三个事件分别为B
1、B
2、B
3,则
P(B
1)=P(A
0•A
1+A
1•A
0)
=2P(A
0)P(A
1)=2×0.6×0.1=0.12,
P(B
2)=P(A
1•A
2+A
2•A
1)
=2P(A
1)P(A
2)=2×0.1×0.3=0.06,
P(B
3)=P(A
1•A
1)=[P(A
1)]
2=0.1
2=0.01,
所以该顾客获得奖金数不小于100元的概率
P′=P(B
1+B
2+B
3)=P(B
1)+P(B
2)+P(B
3)=0.12+0.06+0.01=0.19.
分析:顾客购买一件产品,获一等奖为事件A
1,获二等奖为事件A
2,不获奖为事件A
0(1)该顾客购买2件产品,中奖的对立事件是:该顾客购买2件产品不中奖即事件A
0•A
0,代入概率公式可求
(2)该顾客获得奖金数可能值为100元、120元、200元,,依次记这三个事件分别为B
1、B
2、B
3,则B
1=A
0•A
1+A
1•A
0;B
2=A
1•A
2+A
2•A
1;B
3=A
1•A
1利用相互独立事件及互斥事件的概率可求
点评:本题主要考查了相互独立事件的 概率的求解公式的运用:若事件A,B相互独立,则A与

,
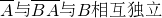
;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.而利用了对立事件的概率公式可简化运算,减少运算量.


 ,
,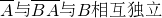 ;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.而利用了对立事件的概率公式可简化运算,减少运算量.
;P(AB)=P(A)P(B);还考查了对一些复杂事件的分解:即对一个事件分解成几个互斥事件的和,本题是把相互独立与互斥结合的综合考查.而利用了对立事件的概率公式可简化运算,减少运算量. 

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 的右焦点,且平行于经过一、三象限的渐近线的直线方程是
的右焦点,且平行于经过一、三象限的渐近线的直线方程是