将函数y＝f(x)图象上每个点的纵坐标保持不变，横坐标伸长到原来的2倍，然后再将整个图象沿x轴向左平移
个单位，得到的曲线与y＝
sinx图象相同，则y＝f(x)的函数表达式为( )．
A．y＝
sin
B．y＝
sin2
C．y＝
sin
D．y＝
sin
科目：高中数学 来源：陕西省铁一中2012届高三第二次模拟考试数学理科试题 题型：044
已知平面向量
＝(cos
，sin)，
＝(cosx，sinx)，
＝(sin，－cos)，其中0＜＜π，且函数f(x)＝(·)cosx＋(·)sinx的图象过点(
，1)．
(1)求的值；
(2)将函数y＝f(x)图象上各点的横坐标变为原来的的2倍，纵坐标不变，得到函数y＝g(x)的图象，求函数y＝g(x)在[0，
]上的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源：河北省衡水中学2012届高三上学期五调考试数学理科试题 题型：044
设函数f(x)＝a2x2(a＞0)，g(x)＝blnx．
(1)将函数y＝f(x)图象向右平移一个单位即可得到函数y＝φ(x)的图象，试写出y＝φ(x)的解析式及值域；
(2)关于x的不等式(x－1)2＞f(x)的解集中的整数恰有3个，求实数a的取值范围；
(3)对于函数f(x)与g(x)定义域上的任意实数x，若存在常数k，m，使得f(x)≥kx＋m和g(x)≤kx＋m都成立，则称直线y＝kx＋m为函数f(x)与g(x)的“分界线”．设a＝
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：广东省揭阳第一中学2012届高三第一次阶段考试数学文科试题 题型：044
设函数
f(x)＝a2x2(a＞0)，g(x)＝blnx．(1)
将函数y＝f(x)图象向右平移一个单位即可得到函数y＝φ(x)的图象，试写出y＝φ(x)的解析式及值域；(2)
关于x的不等式(x－1)2＞f(x)的解集中的整数恰有3个，求实数a的取值范围；(3)
对于函数f(x)与g(x)定义域上的任意实数x，若存在常数k，m，使得f(x)≥kx＋m和g(x)≤kx＋m都成立，则称直线y＝kx＋m为函数f(x)与g(x)的“分界线”．设
，b＝e，试探究f(x)与g(x)是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝2sin(2x＋
)，将函数y＝f(x)图象上各点的纵坐标保持不变，横坐标先缩短到原来的
倍，把所得图象再向左平移个单位，得到函数y＝g(x)的图象，求y＝g(x)在x∈[0，
]上的最小值.
查看答案和解析>>
科目：高中数学 来源：2013届广东省六校联合体高二元月联考理科数学（解析版） 题型：填空题
已知函数f(x)＝Asin(ωx＋φ)(A>0，ω>0,0<φ<π)在x＝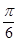
取得最大值2，且函数
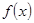的最小正周期为2
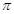.现将函数y＝f(x)图象上各点的横坐标缩小为原来的
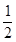，纵坐标不变，再把函数图像向右平移
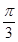个单位，得到函数y＝g(x)的图象，则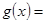
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
sinx逆变换得到f(x)也是函数的图象变换的常用技巧，应熟练掌握．
