
(I)证明:ED为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(II)设![]() 求二面角
求二面角![]() 的大小。
的大小。
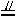
解法一:
(Ⅰ)设O为AC中点,连结EO,BO,则EO![]()
![]() 又
又![]()
![]()
![]() ,所以EO
,所以EO![]() DB,
DB,
EOBD为平行四边行,ED∥OB。 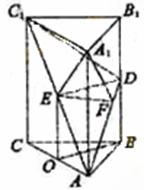
∵AB=BC,∴RO⊥AC,
又平面ABC⊥平面ACC![]() 面ABC,故BO⊥平面ACC
面ABC,故BO⊥平面ACC
∴ED⊥平面ACC
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线。
(Ⅱ)连结A1E,由AA1=AC=![]() AB可知,A1ACC1为正方形,
AB可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面A1ACC1和ED![]() 平面ADC1知平面ADC1⊥平面A1ACC1,
平面ADC1知平面ADC1⊥平面A1ACC1,
∴A1E⊥平面ADC1,作EF⊥AD,垂足为F,连结A![]() 的平面角。
的平面角。
不妨设AA1=2,
则AC=2,AB=![]() ,ED=OB=1,EF=
,ED=OB=1,EF=![]() ,
,![]()
∴∠A1EF=60O。
所以二面角![]() 为60O。
为60O。
解法二:
(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点。
设A(a,0,0),B(0,b,0),B1(0,b,
则C(![]()
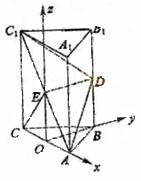
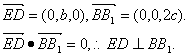
又 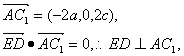
所以ED是异面直线BB1与AC1的公垂线。
(Ⅱ)不妨设A(1,0,0)
则B(0,1,0),C(-1,0,0),A(1,0,2),
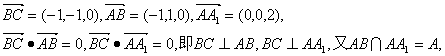
∴ BC⊥面A1AD.
又 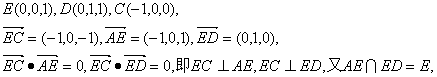
∴ EC⊥面C1AD.
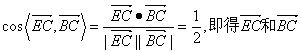 的夹角为600
的夹角为600
所以二面角![]() 为60°。
为60°。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010年湖北省高二上学期期中考试数学理卷 题型:解答题
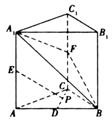
(本小题满分12分)如图所示,在直三棱柱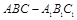 中,
中,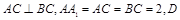 、
、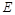 、
、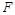 分别是
分别是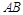 、
、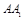 、
、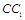 的中点,
的中点,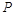 是
是 上的点.
上的点.
(1)求直线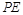 与平面
与平面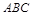 所成角的正切值的最大值;
所成角的正切值的最大值;
(2)求证:直线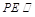 平面
平面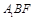 ;
;
(3)求直线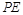 与平面
与平面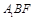 的距离.
的距离.
|
查看答案和解析>>
科目:高中数学 来源: 题型:
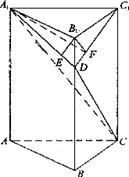
题(19)图
(Ⅰ)求异面直线DE与B1C1的距离;
(Ⅱ)若BC=![]() ,求二面角A1-DC1-B1的平面角的正切值.
,求二面角A1-DC1-B1的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
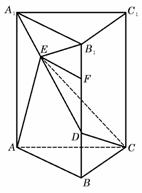
题(19)图
(Ⅰ)异面直线A1D与B1C1的距离;
(Ⅱ)四棱锥C-ABDE的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)如图所示,在直三棱柱![]() 中,
中,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 上的点.
上的点.
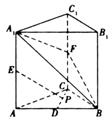 (1)求直线
(1)求直线![]() 与平面
与平面![]() 所成角的正切值的最大值;
所成角的正切值的最大值;
|
(3)求直线![]() 与平面
与平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com