
在三棱锥 中,侧棱长均为
中,侧棱长均为 ,底边
,底边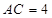 ,
, ,
, ,
,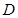 、
、 分别为
分别为 、
、 的中点.
的中点.
(1)求三棱锥 的体积;
的体积;
(2)求二面角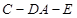 的平面角.
的平面角.
(1)三棱锥 的体积为
的体积为 ;(2)二面角
;(2)二面角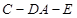 的平面角的大小为
的平面角的大小为 .
.
解析试题分析:(1)由于三棱锥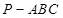 的侧棱长都相等,可以得到点
的侧棱长都相等,可以得到点 在平面
在平面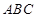 内的射影点为
内的射影点为 的外心,而由于
的外心,而由于 的三条底边满足勾股定理,可知
的三条底边满足勾股定理,可知 为直角三角形
为直角三角形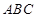 的斜边,从而可以知道
的斜边,从而可以知道 的中点
的中点 即为直角三角形
即为直角三角形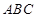 的外心,然后利用勾股定理求出
的外心,然后利用勾股定理求出 ,并且计算出直角三角形
,并且计算出直角三角形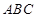 的面积,最后利用锥体的体积公式计算此三棱锥的体积;(2)解法一是在(1)中的基础上,利用
的面积,最后利用锥体的体积公式计算此三棱锥的体积;(2)解法一是在(1)中的基础上,利用 平面
平面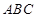 ,得到平面
,得到平面 平面
平面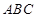 ,然后在平面
,然后在平面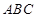 内作
内作 于点
于点 ,利用平面与平面垂直的性质定理得到
,利用平面与平面垂直的性质定理得到 平面
平面 ,从而得到
,从而得到 ,再从点
,再从点 在平面
在平面 内作
内作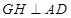 于点
于点 ,并连接
,并连接 ,利用三垂线法得到
,利用三垂线法得到 为二面角
为二面角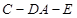 的平面角,最后在直角三角形
的平面角,最后在直角三角形 中计算
中计算 的大小;解法二是以
的大小;解法二是以 为原点,以
为原点,以 为
为 轴建立空间直角坐标系,利用空间向量法求二面角
轴建立空间直角坐标系,利用空间向量法求二面角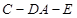 的平面角的大小.
的平面角的大小.
试题解析:(1)取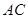 的中点
的中点 ,连接
,连接 ,
,
易得: ,
, ,
,  ,
, .
. .
.
又

 平面
平面 ,
,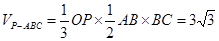
(2)法一:作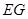 ⊥
⊥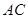 ,
, ⊥
⊥ 于
于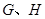 点,连接
点,连接

 平面
平面 ,
, 平面
平面 ,
,
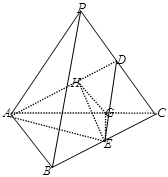
又

 平面
平面 .
.
∵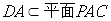 , ∴
, ∴
又

 平面
平面 ,
,
∵ ,∴
,∴ ,
,
∴


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图,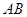 是圆柱体
是圆柱体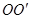 的一条母线,
的一条母线,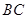 过底面圆的圆心
过底面圆的圆心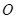 ,
,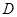 是圆
是圆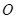 上不与点
上不与点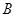 、
、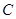 重合的任意一点,已知棱
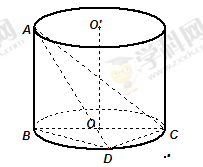
重合的任意一点,已知棱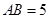 ,
,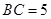 ,
,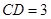 .
.
(1)求证: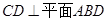 ;
;
(2)将四面体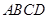 绕母线
绕母线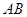 转动一周,求
转动一周,求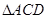 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是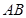 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.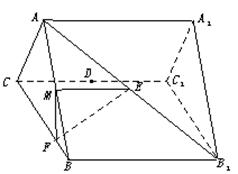
(1)求证:BB1∥平面EFM;
(2)求四面体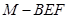 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点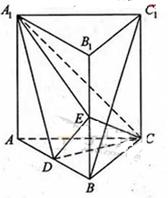
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=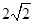 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
(1)求证:AC⊥BB1;
(2)若P是棱B1C1的中点,求平面PAB将三棱柱分成的两部分体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高速公路收费站入口处的安全标识墩如图1所示。墩的上半部分是正四棱锥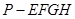 ,下半部分是长方体
,下半部分是长方体 。图2、图3分别是该标识墩的正(主)视图和俯视图。
。图2、图3分别是该标识墩的正(主)视图和俯视图。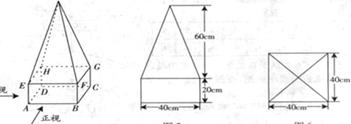
图1 图2 图3
(1)请在正视图右侧画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com