
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点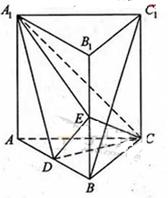
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=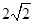 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
(Ⅰ)详见解析;(Ⅱ)三棱锥C一A1DE的体积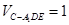 .
.
解析试题分析:(Ⅰ)证明:BC1//平面A1CD,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,注意到D,分别是AB,的中点,可考虑利用三角形的中位线平行,连结 交
交 于点F,则F为
于点F,则F为 中点,连结DF,则
中点,连结DF,则 ∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知
∥DF,从而可证;(Ⅱ)求三棱锥C一A1DE的体积.求体积,关键是找高,由已知 =2,
=2,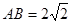 ,可知三角形
,可知三角形 是等腰直角三角形,又因为
是等腰直角三角形,又因为 是直三棱柱,则
是直三棱柱,则 ,
, 即为高,有平面几何知识可得
即为高,有平面几何知识可得 是直角三角形,可求得面积,从而可得体积.
是直角三角形,可求得面积,从而可得体积.
试题解析:(Ⅰ)连结 交
交 于点F,则F为
于点F,则F为 中点,又D是AB中点,连结DF,则
中点,又D是AB中点,连结DF,则 ∥DF
∥DF
因为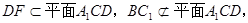 所以
所以 ∥平面
∥平面
(Ⅱ)因为 是直三棱柱,所以,
是直三棱柱,所以,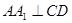 ,由已知AC=CB,D为AB的中点,所以
,由已知AC=CB,D为AB的中点,所以 ,又
,又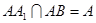 ,于是
,于是 .由
.由 =2,
=2,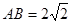 得
得 ,
,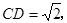
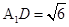 ,
,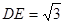 ,
,
 E=3,
E=3,
故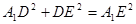 ,
,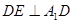 ,所以
,所以 (12分)
(12分)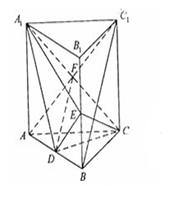
考点:线面平行的判定,几何体的体积.


科目:高中数学 来源: 题型:解答题
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.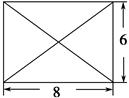
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,PA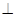 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.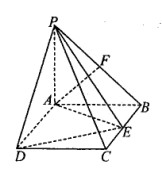
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE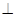 AF.
AF.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
直三棱柱ABC-A1B1C1中,AB=AA1,∠CAB=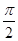 .
.
(1)证明:CB1⊥BA1;
(2)已知AB=2,BC=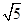 ,求三棱锥C1-ABA1的体积.
,求三棱锥C1-ABA1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com