
如图,三棱柱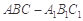 中,侧棱与底面垂直,
中,侧棱与底面垂直,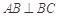 ,
,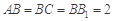 ,
,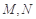 分别是
分别是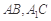 的中点
的中点
(1)求证: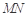 ∥平面
∥平面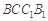 ;
;
(2)求证: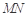 ⊥平面
⊥平面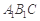 ;
;
(3)求三棱锥的体积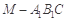 的体积.
的体积.
(1)证明过程详见解析;(2)证明过程详见解析;(3)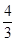 .
.
解析试题分析:本题主要以三棱柱为几何背景考查线面平行、线面垂直和几何体体积等基础知识,考查空间想象能力、运算能力和推理论证能力.第一问,先根据题意作出辅助线,在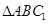 中,利用中位线的性质得
中,利用中位线的性质得 ,再由线面平行的判定,得证;第二问,由已知条件可以判断四边形
,再由线面平行的判定,得证;第二问,由已知条件可以判断四边形 是正方形,所以对角线互相垂直,所以
是正方形,所以对角线互相垂直,所以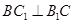 ,又由于第一问得
,又由于第一问得 ,所以
,所以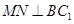 ,再由已知证
,再由已知证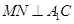 即可,由已知边长,得
即可,由已知边长,得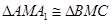 ,所以
,所以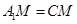 ,所以
,所以 为等腰三角形,而
为等腰三角形,而 为中点,所以
为中点,所以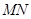 为高,得证,再利用线面垂直的判定即可得证;第三问,利用等体积法将三棱锥进行转化,找到已知条件求体积.
为高,得证,再利用线面垂直的判定即可得证;第三问,利用等体积法将三棱锥进行转化,找到已知条件求体积.
试题解析:(1)证明:连结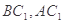 ,显然
,显然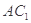 过点
过点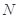
∵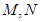 分别是
分别是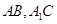 的中点, ∴
的中点, ∴ ,
,
又 平面
平面 ,
,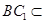 平面
平面 ,∴
,∴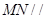 平面
平面 ,
,
(2)∵三棱柱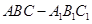 中,侧棱与底面垂直,
中,侧棱与底面垂直,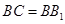 ,
,
∴四边形 是正方形,∴
是正方形,∴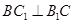 ,
,
由(1)知 ,∴
,∴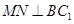 ,
,
连结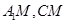 ,由
,由 ,知
,知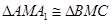 ,
,
∴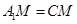 ,又易知
,又易知 是
是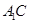 的中点,∴
的中点,∴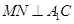 ,
,
∴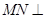 平面
平面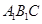 .
.
(3)因为 ,所以三棱锥
,所以三棱锥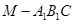 与三棱锥
与三棱锥 的体积相等,
的体积相等,
故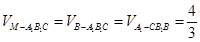 .
.
考点:1.中位线的性质;2.线面平行的判定;3.三角形全等;4.线面垂直的判定;5.等体积法.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
如图,正三棱柱ABC—A1B1C1的各棱长都相等,M、E分别是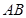 和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
和AB1的中点,点F在BC上且满足BF∶FC=1∶3.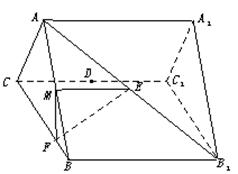
(1)求证:BB1∥平面EFM;
(2)求四面体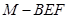 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点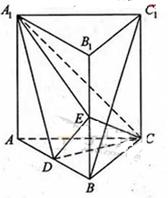
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=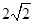 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在三棱柱ABC-A1B1C1中,A1B⊥平面ABC,AB⊥AC.
(1)求证:AC⊥BB1;
(2)若P是棱B1C1的中点,求平面PAB将三棱柱分成的两部分体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是一个直三棱柱被削去一部分后的几何体的直观图与三视图中的侧视图、俯视图.在直观图中,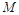 是
是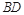 的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.又已知侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.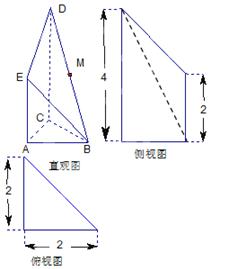
(1)求证:EM∥平面ABC;
(2)试问在棱DC上是否存在点N,使NM⊥平面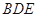 ? 若存在,确定
? 若存在,确定
点N的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在三棱锥A—BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD= ,BD=CD=1,另一个侧面ABC是正三角形.
,BD=CD=1,另一个侧面ABC是正三角形.
(1)当正视图方向与向量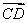 的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
的方向相同时,画出三棱锥A—BCD的三视图;(要求标出尺寸)
(2)求二面角B—AC—D的余弦值;
(3)在线段AC上是否存在一点E,使ED与平面BCD成30°角? 若存在,确定点E的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面四边形ABCD中, ABC为正三角形,
ABC为正三角形, ADC为等腰直角三角形,AD=DC=2,将
ADC为等腰直角三角形,AD=DC=2,将 ABC沿AC折起,使点B至点P,且PD=2
ABC沿AC折起,使点B至点P,且PD=2 ,M为PA的中点,N在线段PD上。
,M为PA的中点,N在线段PD上。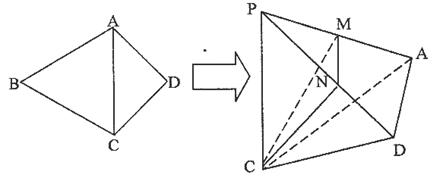
(I)若PA 平面CMN,求证:AD//平面CMN;
平面CMN,求证:AD//平面CMN;
(II)求直线PD与平面ACD所成角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com