
函数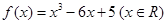 ,若关于
,若关于 的方程
的方程 有三个不同实根,则
有三个不同实根,则 的取值范围是
的取值范围是
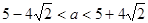
解析试题分析:因为,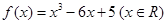 ,所以f′(x)=3(x2-2),
,所以f′(x)=3(x2-2),
令f′(x)=0,得x1=-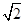 ,x2=
,x2=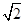 ,
,
∴当 x<-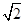 或x>
或x>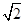 时,f′(x)>0,
时,f′(x)>0,
当-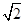 <x<
<x<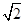 时,f′(x)<0,
时,f′(x)<0,
∴f(x)的单调递增区间是 (-∞,-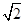 )和(
)和(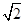 ,+∞),单调递减区间是 (-
,+∞),单调递减区间是 (-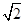 ,
,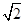 ),
),
当 x=-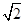 ,f(x)有极大值5+4
,f(x)有极大值5+4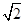 ;当 x=
;当 x=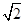 ,f(x)有极小值5-4
,f(x)有极小值5-4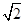 ,
,
由上分析可知y=f(x)图象的大致形状及走向,
∴当 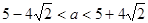 时,直线y=a与y=f(x)的图象有3个不同交点,
时,直线y=a与y=f(x)的图象有3个不同交点,
即方程f(x)=α有三解.
故答案为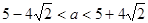 。
。
考点:方程的根,利用导数研究函数的图象、单调性、极值。
点评:中档题,本题通过利用导数研究函数的单调性、图象、极值等,明确了函数的图象大致形态,从而确定得到参数a的取值范围。很好地体现了数形结合、转化与化归的思想方法,具有较强的代表性。


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com