
已知数列{an}成等比数列,且an>0.
(1)若a2-a1=8,a3=m.
①当m=48时,求数列{an}的通项公式;
②若数列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+…+ak+1- (ak+ak-1+…+a1 )=8,k∈N*,
求a2k+1+a2k+2+…+a3k的最小值.
解:设公比为q,则由题意,得q>0.
(1)①由a2-a1=8,a3=m=48,得
解之,得  或
或
所以数列{an}的通项公式为an=8(2- )(3+
)(3+ )n-1,或an=8(2+
)n-1,或an=8(2+ )(3-
)(3- )n-1.
)n-1.
②要使满足条件的数列{an}是唯一的,即关于a1与q的方程组 有唯一正数解,即方程8q2-mq+m=0有唯一解.
有唯一正数解,即方程8q2-mq+m=0有唯一解.
由△=m2-32m=0,a3=m>0,所以m=32,此时q=2.
经检验,当m=32时,数列{an}唯一,其通项公式是an=2n+2.
(2)由a2k+a2k-1+…+ak+1- (ak+ak-1+…+a1 )=8,
得a1(qk-1)(qk-1+qk-2+…+1)=8,且q>1.
a2k+1+a2k+2+…+a3k=a1q2k(qk-1+qk-2+…+1)
= =
= ≥32,
≥32,
当且仅当  ,即q=
,即q= ,a1=8(
,a1=8( -1)时,
-1)时,
a2k+1+a2k+2+…+a3k的最小值为32.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
某公司的广告费支出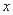 与销售额
与销售额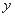 (单位:万元)之间有下列对应数据:由资料显示
(单位:万元)之间有下列对应数据:由资料显示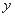 对
对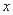 呈线性相关关系。
呈线性相关关系。
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
根据上表提供的数据得到回归方程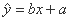 中的
中的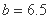 ,预测销售额为115万元时约
,预测销售额为115万元时约
需 万元广告费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com