解:(1)由题意有|PM|=|F
2M|
∴|MF
1|+|MF
2|=|PF
1|=4
∴点M的轨迹是以F
1、F
2为焦点的椭圆.
其方程为

(2)设l的方程为
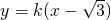
,
(若l的斜率不存在,则
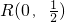
,
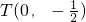
,∴|RT|=1,不合题意)
代入x
2+4y
2-4=0整理有
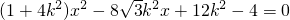
设R(x
1,y
1),T(x
2,y
2)
椭圆右准线方程为:
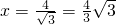
,离心率

.
过R、T作右准线的垂线,设垂足分别为R
2、T
2,则
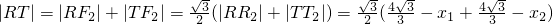
=
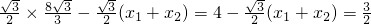
∴
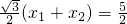
即
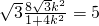
解之有
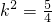
,
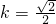
∴l的方程为
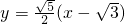
(3)|QF
1|+|QF
2|=4
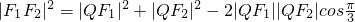
∴12=|QF
1|
2+|QF
2|
2-|QF
1|•|QF
2|
而|QF
1|+|QF
2|=4,
∴|QF
1|
2+|QF
2|
2+2|QF
1|•|QF
2|=16
∴12=16-2|QF
1|•|QF
2|-|QF
1|•|QF
2|
∴
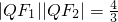
∴S
△F1F2Q=
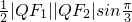
=
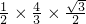
=

.
分析:(1)由题意有|PM|=|F
2M|从而有|MF
1|+|MF
2|=|PF
1|=4,根据椭圆的定义得点M的轨迹是以F
1、F
2为焦点的椭圆.再写出其方程即可;
(2)设l的方程为
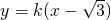
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用线段的比例关系即可求得k值,从而解决问题.
(3)根据三角形中的余弦定理可得12=|QF
1|
2+|QF
2|
2-|QF
1|•|QF
2|而|QF
1|+|QF
2|=4,从而得出
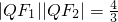
最后利用三角形的面积公式求解即得.
点评:本小题主要考查椭圆的定义、直线与圆锥曲线的综合问题、直线的方程等基础知识,考查运算求解能力,考查数形结合思想、方程思想.属于中档题.

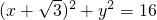 ,
,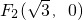 ,在⊙F1上取点P,连接PF2,作出线段PF2的垂直平分线交PF1于M
,在⊙F1上取点P,连接PF2,作出线段PF2的垂直平分线交PF1于M ,当点P在⊙F1上运动时M形成曲线C.(如图)
,当点P在⊙F1上运动时M形成曲线C.(如图) ,求直线l的方程.
,求直线l的方程.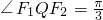 ,求
,求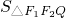 .
.
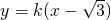 ,
,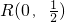 ,
,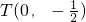 ,∴|RT|=1,不合题意)
,∴|RT|=1,不合题意)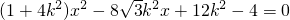
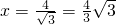 ,离心率
,离心率 .
.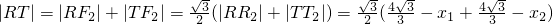
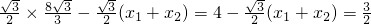
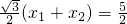 即
即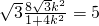
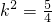 ,
,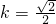
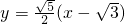
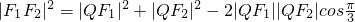
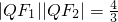
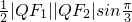 =
=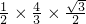 =
= .
.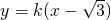 ,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用线段的比例关系即可求得k值,从而解决问题.
,将直线的方程代入椭圆的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用线段的比例关系即可求得k值,从而解决问题.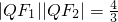


 ,
, ,在⊙F1上取点P,连接PF2,作出线段PF2的垂直平分线交PF1于M,当点P在⊙F1上运动时M形成曲线C.(如图)
,在⊙F1上取点P,连接PF2,作出线段PF2的垂直平分线交PF1于M,当点P在⊙F1上运动时M形成曲线C.(如图) ,求直线l的方程.
,求直线l的方程. ,求
,求 .
.