若方程(1+a)x2-3ax+4a=0的所有根均小于1,求实数a的范围.
【答案】
分析:方程(1+a)x
2-3ax+4a=0是一个类二次方程,我们要首先分1+a=0和1+a≠0两种情况进行分类讨论,当方程为二次方程时所有根均小于1,情况比较复杂,故我们可以先讨论方程的两根均不小于1的情况,再利用补集思想求出满足条件的实数a的范围.
解答:解:若1+a=0,即a=-1
则原方程可化为:3x-4=0,解得x=

,不满足要求
若1+a≠0,即a≠-1时,
若方程(1+a)x
2-3ax+4a=0有根,则△=9a
2-16a
2-16a≥0
即
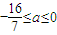
若方程(1+a)x
2-3ax+4a=0的所有根均不小于1
则
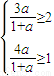
,即
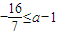
故方程(1+a)x
2-3ax+4a=0的所有根均小于1时,-1<a≤0
即实数a的范围为,-1<a≤0
点评:本题考查的知识点是一元二次方程的根的分布与系数的关系,利用“正难则反”的思想,先求方程(1+a)x
2-3ax+4a=0的所有根均不小于1时,实数a的范围,再利用补集思想进行解答是本题的关键.

 ,不满足要求
,不满足要求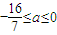
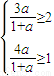 ,即
,即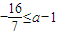


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案