【答案】
分析:第1问在一个区间有唯一零点需满足两个条件:(1)在这个区间单调;(2)区间端点函数值异号.第2问要利用数学归纳法证明,关键在于x
n+1=f(x
n)的应用.第3问要分k=1,k≥2,情况进行证明为m∈N
*时证明做铺垫,在其中结合不等式证明方法中的放缩法进行适当的放缩,还有等比数列求和公式.
解答:解:(Ⅰ)证明:①f(x)=x?x
3+ax-1=0.…(1分)
令h(x)=x
3+ax-1,则h(0)=-1<0,

,
∴
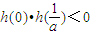
.…(2分)
又h′(x)=3x
2+a>0,∴h(x)=x
3+ax-1是R上的增函数.…(3分)
故h(x)=x
3+ax-1在区间
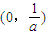
上有唯一零点,
即存在唯一实数
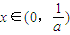
使f(x
)=x
.…(4分)
(Ⅱ)(i)当n=1时,x
1=0,
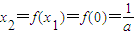
,由①知
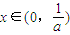
,即x
1<x
<x
2成立;…(5分)
设当n=k(k≥2)时,x
2k-1<x
<x
2k,注意到
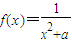
在(0,+∞)上是减函数,且x
k>0,
故有:f(x
2k-1)>f(x
)>f(x
2k),即x
2k>x
>x
2k+1∴f(x
2k)<f(x
)<f(x
2k+1),…(7分)
即x
2k+1<x
<x
2k+2.这就是说,n=k+1时,结论也成立.
故对任意正整数n都有:x
2n-1<x
<x
2n.…(8分)
(ii)当a=2时,由x
1=0得:
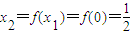
,
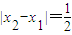
…(9分)
当k=1时,
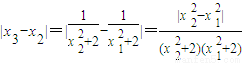
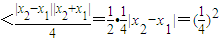
…(10分)
当k≥2时,∵
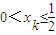
,
∴
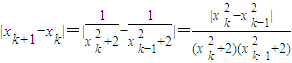
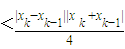
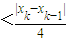
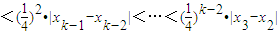
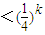
…(12分)
对?m∈N
*,
|x
m+k-x
k|=|(x
m+k-x
m+k-1)+(x
m+k-1-x
m+k-2)+…+(x
k+1-x
k)|≤|x
m+k-x
m+k-1|+|x
m+k-1-x
m+k-2|+…+|x
k+1-x
k|
…(13分)
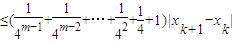
=
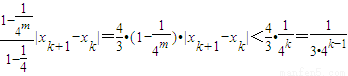
…(14分)
点评:本题考查了在一个区间有唯一零点需满足的条件,往往会出现只对端点函数值异号,而忽略单调的条件出现错误.第2问考查了数学归纳法证明,难点在于由 n=k时成立,如何得出n=k+1也成立.第3问难点在于|x
m+k-x
k|=|(x
m+k-x
m+k-1)+(x
m+k-1-x
m+k-2)+…+(x
k+1-x
k)|这个式子的得出.总体来说本题比较难.

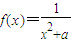 .
. ,使f(x)=x;
,使f(x)=x;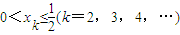 ,证明:对任意m∈N*都有:
,证明:对任意m∈N*都有: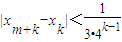 .
. ,
,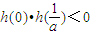 .…(2分)
.…(2分)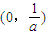 上有唯一零点,
上有唯一零点,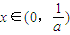 使f(x)=x.…(4分)
使f(x)=x.…(4分)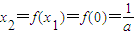 ,由①知
,由①知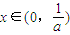 ,即x1<x<x2成立;…(5分)
,即x1<x<x2成立;…(5分)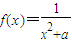 在(0,+∞)上是减函数,且xk>0,
在(0,+∞)上是减函数,且xk>0,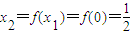 ,
,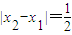 …(9分)
…(9分)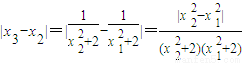
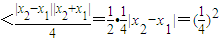 …(10分)
…(10分)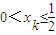 ,
,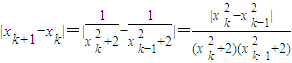
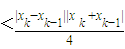
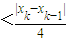
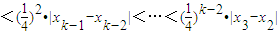
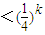 …(12分)
…(12分)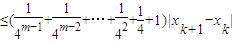
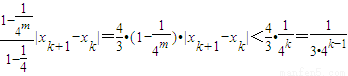 …(14分)
…(14分)

