已知数列{an}中,a1=2,a2=3,其前n项和Sn满足Sn+1+Sn-1=2Sn+1(n≥2,n∈N*).
(1)求证:数列为等差数列,并求的通项公式;
(2)bn=2n•an,求数列{bn}的前n项和Tn;
(3)cn=4n+(-1)n-1λ•2a(λ为非零整数,n∈N*),试确定λ的值,使得数列{cn}是递增数列.
【答案】
分析:(1)利用数列递推式,可得(S
n+1-S
n)-(S
n-S
n-1)=1(n≥2,n∈N
*),由此可得结论,并可求通项公式;
(2)利用错位相减法,求得数列{b
n}的前n项和,代入不等式,利用函数的单调性,即可求n的取值范围;
(3)要使c
n+1>c
n恒成立,即3×4
n-3(-1)
n-1λ2
n+1>0恒成立,分离参数,分类讨论,即可求得结论.
解答:(1)证明:由已知得,
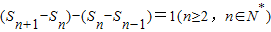
,----------------(1分)
即

,且a
2-a
1=1.----------------(2分)
所以数列{a
n}是以a
1=2为首项,公差为1的等差数列,
所以a
n=n+1.------------------(4分)
(2)解:由(1)知
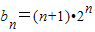
,它的前n项和为T
n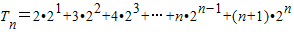
.①
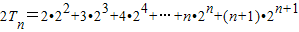
.②
①-②得,
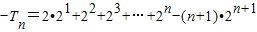
-----------------(6分)=

∴

.--------------------(8分)
(3)解:∵a
n=n+1,∴

,
要使c
n+1>c
n恒成立,即3×4
n-3(-1)
n-1λ2
n+1>0恒成立,∴(-1)
n-1λ<2
n-1恒成立,…(12分)
(i)当n为奇数时,即λ<2
n-1恒成立,当且仅当n=1时,2
n-1有最小值为1,∴λ<1.
(ii)当n为偶数时,即λ>-2
n-1恒成立,当且仅当n=2时,-2
n-1有最大值-2,∴λ>-2.
∴-2<λ<1,又λ为非零整数,则λ=-1.…(15分)
综上所述:存在λ=-1,使得对任意的n∈N
*,都有c
n+1>c
n.…(16分)
点评:本题考查数列递推式,考查数列的通项与求和,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

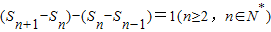 ,----------------(1分)
,----------------(1分) ,且a2-a1=1.----------------(2分)
,且a2-a1=1.----------------(2分)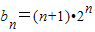 ,它的前n项和为Tn
,它的前n项和为Tn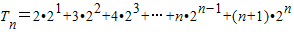 .①
.①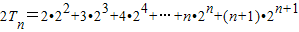 .②
.②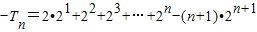 -----------------(6分)=
-----------------(6分)= ∴
∴ .--------------------(8分)
.--------------------(8分) ,
,

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案