
已知动圆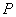 过定点
过定点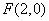 且与直线
且与直线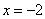 相切,圆心
相切,圆心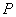 的轨迹为曲线
的轨迹为曲线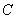
(I)求轨迹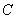 的方程;
的方程;
(Ⅱ)①过定点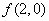 作互相垂直的直线
作互相垂直的直线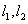 分别交轨迹
分别交轨迹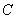 于点
于点 和点
和点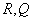 ,求四边形
,求四边形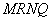 面积的最小值;
面积的最小值;
②定点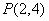 ,动点
,动点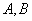 是轨迹
是轨迹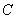 上的三个点,且满足
上的三个点,且满足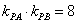 试问
试问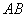 所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由
所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由
解:(1)由题意: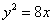 为点M的轨迹方程。
为点M的轨迹方程。
(2)由题易知直线l1,l2的斜率都存在,且不为0,
不妨设,MN方程为y=k(x-2)与y2=8x联立得:
k2x2-(4k2+8)x+4k2=0,设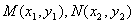
∴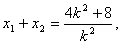
由抛物线定义知:|MN|=|MF|+|NF|
同理RQ的方程为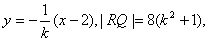
∴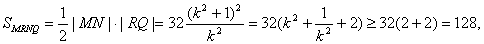
当且仅当k2=1,k=±1时取“=”,故四边形MRNQ的面积的最小值为128.
(3)设
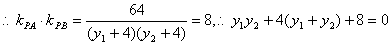 ········(※)
········(※)
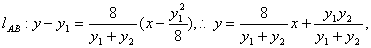
则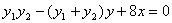 ,与(※)比较可知,直线AB过定点(1,-4)
,与(※)比较可知,直线AB过定点(1,-4)
法2:
设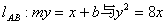 联立得:
联立得: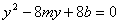 由△>0得2m2>b。
由△>0得2m2>b。
设y1+y2=8m,y1·y2=8b,又由kPA·kPB=8
即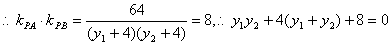
∴4m+b+1=0
∴lAB:my=x-4m-1即m(y+4)=x-1,∴直线AB过定点(1,-4)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
己知函数f(x)=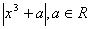 在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-
在[-1,1]上的最大值为M(a) ,若函数g(x)=M(x)-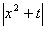 有4个零点,则实数t的取值范围为。
有4个零点,则实数t的取值范围为。
A. (1,  ) B. (
) B. (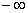 1, -1) C. (
1, -1) C. (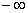 1, -1)
1, -1)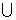 (1,
(1,  ) D. (
) D. (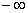 1, -1)
1, -1)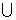 (1, 2)
(1, 2)
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法错误的是
A.命题“若x2—4x+3=0,则x=3”的逆否命题是“若x≠3,则x2-4x+3≠0”
B.“x>l”是“|x|>0”的充分不必要条件
C.若p∧q为假命题,则p、g均为假命题
D.命题P:“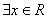 ,使得x2+x+1<0”,则
,使得x2+x+1<0”,则
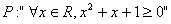
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数 的定义域为
的定义域为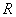 ,若存在常数
,若存在常数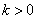 ,使
,使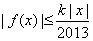 对于一切
对于一切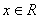 均成立,则称
均成立,则称 为“好运”函数。给出下列函数:①
为“好运”函数。给出下列函数:①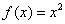 ; ②
; ②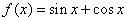 ;
;
③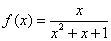 ; ④
; ④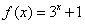 。其中
。其中 是“好运”函数的序号是( )
是“好运”函数的序号是( )
A. ①② B.①③ C. ③ D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com