练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在区间［－1，1］上任取两数a、b，求二次方程x2+ax+b=0的两根，用随机模拟法估算：

    （1）都是实数的概率；（2）都是正数的概率.

    解析：根据两根满足的条件得到a、b满足的关系，利用随机模拟求得概率.

    据题意－1≤a≤1，－1≤b≤1，以a为横坐标、b为纵坐标，得到一个边长为2的正方形，如图所示.

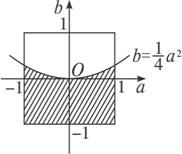
    （1）若a、b都是实数，则Δ=a2－4b≥0，即b≤，利用随机模拟求概率.

    ①利用计算机或计算器产生0至1区间的两组随机数，a1=rand()，b1=rand()；

    ②经平移和伸缩变换，a=a1* 2－1，b=b1* 2－1；

    ③数出满足b≤的数组数N1.

    则所求概率近似为（N为总数组数）.

    （2）如下图，若两根都是正数，则有

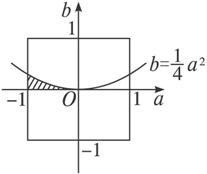
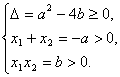
    即b≤且a＜0，b＞0.

    在第（1）问求出的随机数中数出满足b≤且a＜0，b＞0的数组数N2，则所求概率近似为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若偶函数f（x）在区间（-∞，-1]上是增函数，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    二次函数y=f（x）满足：①f（0）=1；②f（x+1）-f（x）=2x．
    （1）求f（x）的解析式；
    （2）求f（x）在区间[-1，1]上的最大值和最小值；
    （3）设g（x）=f（x-a），求g（x）在区间[-1，1]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）定义在区间（-1，1）上，f（
    1
    2
    ）=-1，且当x，y∈（-1，1）时，恒有f（x）-f（y）=f（
    x-y
    1-xy
    ），又数列{an}满足：a1=
    1
    2
    ，an+1=
    2an
    1+
    a
    2
    n
    ．
    （I）证明：f（x）在（-1，1）上为奇函数；
    （II）求f（an）关于n的函数解析式；
    （III）令g（n）=f（an）且数列{an}满足bn=
    1
    g(n)
    ，若对于任意n∈N+，都有b1+b2+…+bn＜t2-3t恒成立，求实数t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•绵阳一模）已知函数f（x）定义在区间（-1，1）上，f（
    1
    2
    ）=-1，且当x，y∈（-1，1）时，恒有f（x）-f（y）=f（
    x-y
    1-xy
    ）．又数列{an}满足，a1=
    1
    2
    ，an+1=
    2an
    1+an2
    ．
    （I ）证明：f（x）在（-1，1）上是奇函数
    （ II ）求f（an）的表达式；
    （III）设bn=
    1
    2log2|f(an+1)
    ，Tn为数列{bn}的前n项和，若T2n+1-Tn≤
    m
    15
    （其中m∈N*）对N∈N*恒成立，求m的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•绵阳一模）已知函数f（x）定义在区间（-1，1）上，f（
    1
    2
    ）=-1，且当x，y∈（-1，1）时，恒有f（x）-f（y）=f（
    x-y
    1-xy
    ）．又数列{an}满足，a1=
    1
    2
    ，an+1=
    2an
    1+an2
    ．
    （I ）证明：f（x）在（-1，1）上是奇函数
    （ II ）求f（an）的表达式；
    （III）设bn=-
    1
    2f(an)
    ，Tn为数列{bn}的前n项和，试问是否存在正整数m，n，使得
    4Tn-m
    4Tn+1-m
    ＜
    1
    2
    成立？若存在，求出这样的正整数；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案