练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图所示，在以AB为直径的半圆周上，有异于A、B的六个点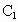、、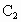、、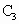、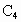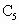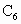，直径AB上有异于A、B的四个点、、、．

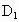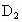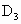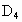    问：(1)以这10个点中的3个点为顶点作三角形可作多少个?其中含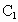点的有多少个?

    (2)以图中的12个点(包括A、B)中的4个为顶点，可作出多少个四边形?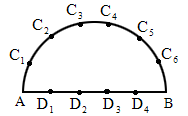
    答案：略
    解析：

    解析：(1)可分三种情况处理：

    ①、、…、这六个点中任取三点可构成一个三角形．

    ②、、…、中任取一点，、、、中任取两点可构成一个三角形．

    ③、、…、中任取两点，、、、中任取一点可构成一个三角形．

    个．

    其中以为顶点的三角形有

    个；

    (2)构成一个四边形，需要四个点，且无三点共线．

    个．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

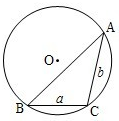    精英家教网通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
    （1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
    （2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
    （3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

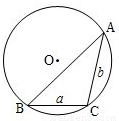
    (2007上海春，20)通常用a、b、c分别表示△ABC的三个内角A、B、C所对边的边长，R表示△ABC的外接圆半径．

    (1)如图所示，在以O为圆心、半径为2的⊙O中，BC和BA是圆的弦，其中BC=2，∠ABC=45°，求弦AB的长；

    (2)在△ABC中，若∠C是钝角，求证：；

    (3)给定三个正实数a、b、R，其中b≤a．问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在、存在一个或存在两个(全等的三角形算作同一个)?在△ABC存在的情况下，用a、b、R表示c．

    查看答案和解析>>

    科目：高中数学 来源：2009-2010学年湖北省武汉二中高一（上）期末数学试卷（解析版） 题型：解答题

    通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
    （1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
    （2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
    （3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．

    查看答案和解析>>

    科目：高中数学 来源：2007年上海市春季高考数学试卷（解析版） 题型：解答题

    通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
    （1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
    （2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
    （3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．

    查看答案和解析>>

    同步练习册答案