【答案】
分析:(Ⅰ)由
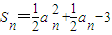
,知
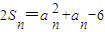
,
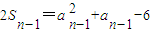
,两式相减整理得:(a
n+a
n-1)(a
n-a
n-1-1)=0,点A
n(n,b
n)在直线l:y=2x+1上,由此能求出数列{a
n},{b
n}的通项公式.
(Ⅱ)由
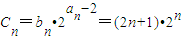
,知T
n=3•2+5•2
2+7•2
3+…+(2n+1)•2
n,由错位相减法能求出T
n.
(Ⅲ)对任意的n∈N
*,不等式
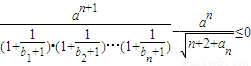
恒成立,令f(n)=
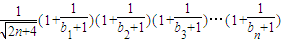
,由此能求出正实数a的取值范围.
解答:解:(Ⅰ)由已知
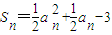
,
∴
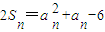
(1)
当n≥2时,
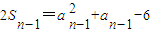
(2)
两式相减整理得:(a
n+a
n-1)(a
n-a
n-1-1)=0,----(2分)
注意到a
n>0,∴a
n-a
n-1-1=0,∴a
n=n+2,
又当n=1时,a
1=S
1,解得a
1=3适合,∴a
n=n+2,----(3分)
点A
n(n,b
n)在直线l:y=2x+1上,∴b
n=2n+1.----(4分)
(Ⅱ)∵
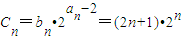
,
∴T
n=c
1+c
2+…+c
n=3•2+5•2
2+7•2
3+…+(2n+1)•2
n
∴
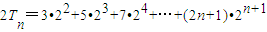
,
错位相减得
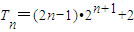
.----(8分)
(Ⅲ)∵对任意的n∈N*不等式
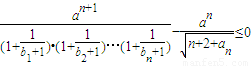
恒成立,
由a>0,即
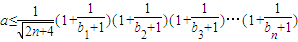
,---(9分)
令f(n)=
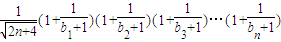
,--(10分)
∴f(n+1)=
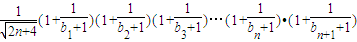
,
∴f(n+1)>f(n),f(n)单调递增,----(12分)
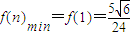
.∴
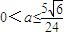
.----(14分)
点评:本题考查数列的通项公式、前n项和公式和实数的取值范围的求法,考查数列、不等式知识,考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

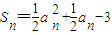 ,(n∈N*),数列{bn}满足:点列An(n,bn)在直线2x-y+1=0
,(n∈N*),数列{bn}满足:点列An(n,bn)在直线2x-y+1=0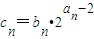 ,求Tn;
,求Tn;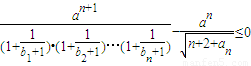 恒成立,求正实数a的取值范围.
恒成立,求正实数a的取值范围.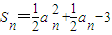 ,知
,知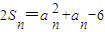 ,
,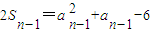 ,两式相减整理得:(an+an-1)(an-an-1-1)=0,点An(n,bn)在直线l:y=2x+1上,由此能求出数列{an},{bn}的通项公式.
,两式相减整理得:(an+an-1)(an-an-1-1)=0,点An(n,bn)在直线l:y=2x+1上,由此能求出数列{an},{bn}的通项公式.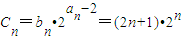 ,知Tn=3•2+5•22+7•23+…+(2n+1)•2n,由错位相减法能求出Tn.
,知Tn=3•2+5•22+7•23+…+(2n+1)•2n,由错位相减法能求出Tn.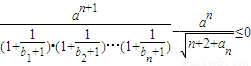 恒成立,令f(n)=
恒成立,令f(n)=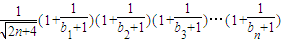 ,由此能求出正实数a的取值范围.
,由此能求出正实数a的取值范围.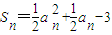 ,
,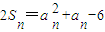 (1)
(1)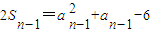 (2)
(2)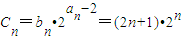 ,
,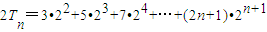 ,
,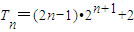 .----(8分)
.----(8分)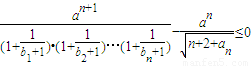 恒成立,
恒成立,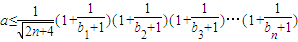 ,---(9分)
,---(9分)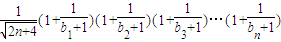 ,--(10分)
,--(10分)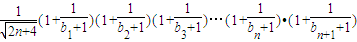 ,
,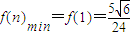 .∴
.∴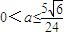 .----(14分)
.----(14分)

 互动英语系列答案
互动英语系列答案