
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
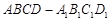 中,
中,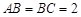 ,过
,过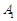 、
、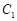 、
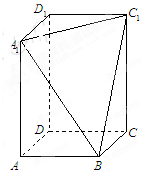
、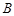 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体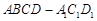 ,且这个几何体的体积为
,且这个几何体的体积为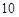 .
.
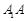 的长;
的长;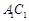 的中点为
的中点为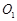 ,求异面直线
,求异面直线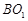 与
与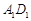 所成角的余弦值.
所成角的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
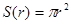 ,周长
,周长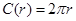 ,若将
,若将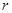 看作是
看作是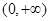 上的变量,则
上的变量,则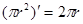 ……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为
……①,这里①式可以用语言表达为:圆的面积函数的导数等于圆的周长函数.对于半径为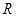 的球,若将
的球,若将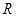 看作
看作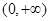 上的变量,请你写出类似于
上的变量,请你写出类似于查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
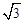 正方形。若PA=2
正方形。若PA=2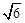 ,则△OAB的面积为______________.
,则△OAB的面积为______________.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
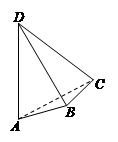
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
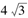 ,BC=
,BC=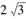 ,且矩形从CD的顶点都在半径为R的球O的球面上,若四棱锥O -ABCD的体积为8,则球O的半径R=
,且矩形从CD的顶点都在半径为R的球O的球面上,若四棱锥O -ABCD的体积为8,则球O的半径R=| A.3 | B.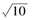 | C.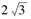 | D.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com