
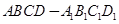 是底面边长为1的正四棱柱,
是底面边长为1的正四棱柱,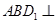 平面
平面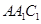
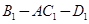 的平面角为120°时,求四棱锥
的平面角为120°时,求四棱锥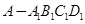 的体积。
的体积。
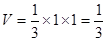 .
.
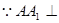 平面
平面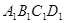 ,
,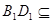 平面
平面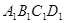 --------------(1分)
--------------(1分)
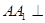
 ,又
,又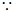
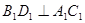 ----------------------------------(2分)
----------------------------------(2分) --------------------------------------------------(3分)
--------------------------------------------------(3分)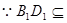 平面
平面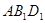
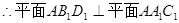 ---------------------------------------------(5分)
---------------------------------------------(5分) ,那么
,那么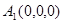 ;
;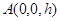 ;
;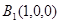 ;
;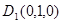 ;
;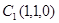 ------(6分)
------(6分)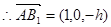 ;
;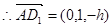 ;
; ;
;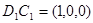 -------(7分)
-------(7分)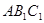 与平面
与平面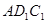 的法向量分别为
的法向量分别为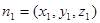 ;
;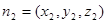 ,那么
,那么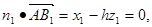 ;
;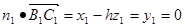 令
令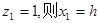
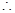
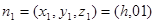 -----------------------------------------------------------------(8分)
-----------------------------------------------------------------(8分)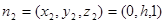 --------------------------------------(9分)
--------------------------------------(9分)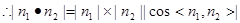
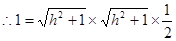 ,
,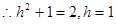 -------------------------------(11分)
-------------------------------(11分)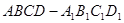 是棱长为1的正方体,且
是棱长为1的正方体,且 的体积
的体积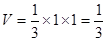 ------------------------------(12分)
------------------------------(12分)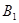 作
作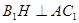 于
于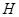 ,连接
,连接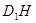 ,
,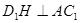 ,
,
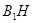 =
=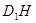 --------------------------------------(7分)
--------------------------------------(7分)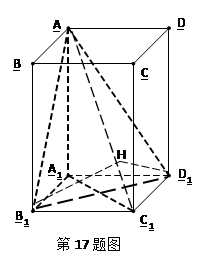 所以
所以 ,且在
,且在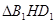 中,由余弦定理可得:
中,由余弦定理可得: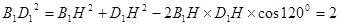
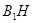 =
=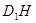 =
=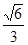 ,又可证得:------------(9分)
,又可证得:------------(9分)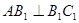 ,所以在
,所以在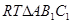 ,由等面积法:
,由等面积法: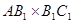 =
=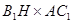 ,
, ------------(9分)
------------(9分)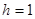 ,---------------------------------------------(11分)
,---------------------------------------------(11分)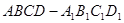 是棱长为1的正方体,且
是棱长为1的正方体,且 的体积
的体积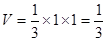 -------------------------------------------(12分)
-------------------------------------------(12分)

科目:高中数学 来源:不详 题型:解答题
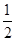 .
.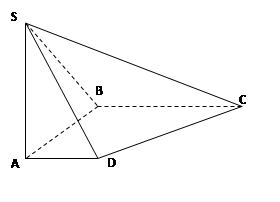
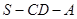 的正切值.
的正切值. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com