
分析 (1)利用等差数列性质及其前n项和公式即可得出;
(2)利用等差数列通项公式及其前n项和公式即可得出Sn;再利用导数研究函数的单调性即可得出.
解答 解:(1)∵数列{an}是等差数列,∴a5+a15=a1+a19=20,
∴S19=$\frac{19({a}_{1}+{a}_{19})}{2}$=$\frac{19×20}{2}$=190.
(2)设等差数列{an}的公差为d.
∵S10=0,a15=25,
∴$\left\{\begin{array}{l}{10{a}_{1}+\frac{10×9}{2}d=0}\\{{a}_{1}+14d=25}\end{array}\right.$,
解得a1=$-\frac{225}{19}$,d=$\frac{50}{19}$.
∴Sn=$-\frac{225}{19}n$+$\frac{n(n-1)}{2}×\frac{50}{19}$=$\frac{25}{19}$(n2-10n),
∴nSn=$\frac{25}{19}$(n3-10n2),
令f(x)=x3-10x2(x≥1).
∴f′(x)=3x2-20x=3x$(x-\frac{20}{3})$,
∴函数f(x)在$[1,\frac{20}{3})$上单调递减;函数f(x)在$(\frac{20}{3},+∞)$上单调递增.
f(6)=63-10×62=-96,f(7)=73-10×72=-147.
∴nSn的最小值是$\frac{25}{19}$×(-147)=$-\frac{3675}{19}$.
点评 本题考查了等差数列的性质通项公式及其前n项和公式、利用导数研究函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0° | B. | 60° | C. | 90° | D. | 180° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
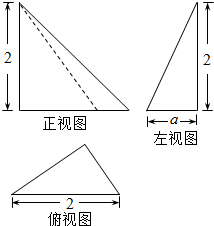
| A. | S是定值,S=8π | B. | S不是定值,有最小值Smin=8π | ||
| C. | S不是定值,有最大值Smax=8π | D. | S不是定值,与a的大小有关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com