
定义在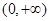 上的函数
上的函数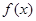 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有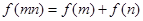 成立,当x>1时,
成立,当x>1时,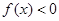 .
.
(1)求证:1是函数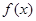 的零点;
的零点;
(2)求证: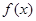 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当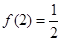 时,解不等式
时,解不等式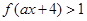 .
.
(3)当a=0时,解集为 ;当a>0时,解集为
;当a>0时,解集为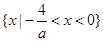 ;
;
当a<0时,解集为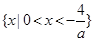 ..
..
【解析】(1)赋值法,求得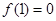 ;(2)注意构造
;(2)注意构造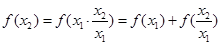 ;
;
(3)由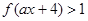 等价于
等价于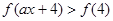 ,分类讨论.
,分类讨论.
解:(1)对于任意的正实数m,n都有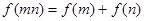 成立,
成立,
所以令m=n=1,则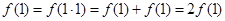 .
.
∴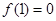 ,即1是函数f(x)的零点.
(3分)
,即1是函数f(x)的零点.
(3分)
(2)设0<x1<x2,则由于对任意正数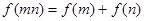 ,
,
所以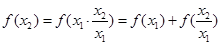 ,即
,即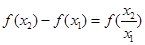
又当x>1时,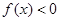 ,而
,而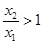 .所以
.所以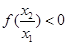 .
.
从而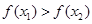 ,因此
,因此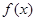 在(0,+∞)上是减函数.
(7分)
在(0,+∞)上是减函数.
(7分)
(3)根据条件有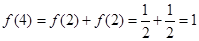 ,
,
所以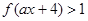 等价于
等价于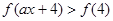 .
.
再由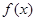 是定义在(0,+∞)上的减函数,所以0<ax+4<4.即
是定义在(0,+∞)上的减函数,所以0<ax+4<4.即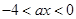 . (9分)
. (9分)
当a=0时,-4<0<0不成立,此时不等式的解集为 ; (10分)
; (10分)
当a>0时,-4<ax<0,即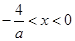 ,此时不等式的解集为
,此时不等式的解集为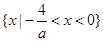 ;
;
当a<0时,-4<ax<0,即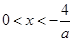 ,此时不等式的解集为
,此时不等式的解集为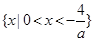 .(12分)
.(12分)


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
(2012年高考(湖北文))定义在![]() 上的函数
上的函数![]() ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列![]() 仍是等比数列,则称
仍是等比数列,则称![]() 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在![]() 上的如下函数:①
上的如下函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
则其中是“保等比数列函数”的![]() 的序号为 ( )
的序号为 ( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考(湖北理))定义在![]() 上的函数
上的函数![]() ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列![]() ,
, ![]() 仍
仍
是等比数列,则称![]() 为“保等比数列函数”. 现有定义在
为“保等比数列函数”. 现有定义在![]() 上的如下函
上的如下函
数:①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() .
.
则其中是“保等比数列函数”的![]() 的序号为 ( )
的序号为 ( )
A.① ② B.③ ④ C.① ③ D.② ④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三第一阶段测试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)
定义在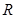 上的函数
上的函数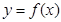 ,对于任意的实数
,对于任意的实数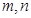 ,恒有
,恒有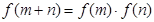 ,且当
,且当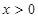 时,
时,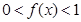 。
。
(1)求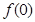 及
及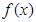 的值域。
的值域。
(2)判断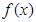 在
在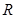 上的单调性,并证明。
上的单调性,并证明。
(3)设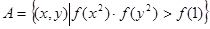 ,
,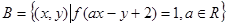 ,
,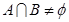 ,求
,求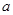 的范围。
的范围。
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二上学期期中考试数学试卷(解析版) 题型:选择题
定义在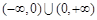 上的函数
上的函数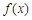 ,如果对于任意给定的等比数列
,如果对于任意给定的等比数列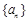 ,
,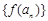 仍是等比数列,则称
仍是等比数列,则称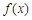 为“保等比数列函数”.现有定义在
为“保等比数列函数”.现有定义在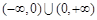 上的如下函数: ①
上的如下函数: ①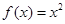 ; ②
; ②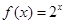 ; ③
; ③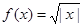 ; ④
; ④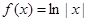 .
.
则其中是“保等比数列函数”的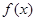 的序号为
的序号为
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中数学 来源:2014届吉林省长春市高一上学期期末考试文科数学试卷(解析版) 题型:解答题
定义在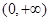 上的函数
上的函数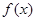 ,对于任意的m,n∈(0,+∞),都有
,对于任意的m,n∈(0,+∞),都有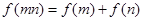 成立,当x>1时,
成立,当x>1时,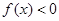 .
.
(1)求证:1是函数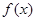 的零点;
的零点;
(2)求证: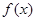 是(0,+∞)上的减函数;
是(0,+∞)上的减函数;
(3)当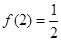 时,解不等式
时,解不等式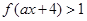 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com