已知f(x)=x3-3x,过点A(1,m) (m≠-2)可作曲线y=f(x)的三条切线,则实数m的取值范围是( )
A.(-1,1)
B.(-2,3)
C.(-1,2)
D.(-3,-2)
【答案】
分析:先设切点坐标,用导数求出切线斜率,再用斜率公式求出切线斜率,两者相等,得到含m的方程,因为过点A(1,m) (m≠-2)可作曲线y=f(x)的三条切线,所以前面所求方程有3解,再借助导数判断何时方程有3解即可.
解答:解;设切点坐标(x
,x
3-3x),
∵f(x)=x
3-3x,∴f′(x)=3x
2-3
∴曲线y=f(x)在(x
,x
3-3x)处的切线斜率为3x
2-3
又∵切线过点A(1,m),∴切线斜率为
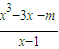
,
∴
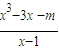
=3x
2-3
即2x
3-3x
2+m+3=0 ①
∵过点A(1,m) (m≠-2)可作曲线y=f(x)的三条切线,
∴方程①有3解.
令ω(x
)=2x
3-3x
2+m+3,则ω(x
)图象与x轴有2个交点,∴ω(x
)的极大值与极小值异号
ω′(x
)=6x
2-6x
,令ω′(x
)=0,得6x
=0或1
∴ω(0)ω(1)<0,即(m+3)(m+2)<0
-3<m<-2
故选D
点评:本题主要考查了导数的几何意义,以及利用导数判断方程根的个数.

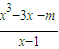 ,
,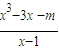 =3x2-3
=3x2-3
