
(本小题满分10分)
已知奇函数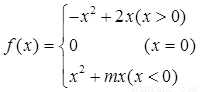
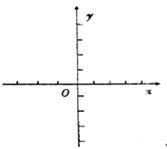
(1)求实数m的值,并在给出的直角坐标系中画出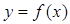 的图象;
的图象;
(2)若函数 在区间[-1,
在区间[-1,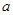 -2]上单调递增,试确定
-2]上单调递增,试确定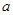 的取值范围.
的取值范围.
(1) m=2.(2)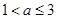
【解析】
试题分析:(1)由奇函数 的定义,对应相等求出m的值;画出图象.
的定义,对应相等求出m的值;画出图象.
(2)根据函数的图象知函数的单调递增区间,从而得到|a|-2的一个不等式,解不等式就求得a 的取值范围.
(1)当x<0时,-x>0,f(x)=-(x)2+2(-x)=-x2-2x,
又f(x)为奇函数,f(x)=-f(-x)=x2+2x,
所以m=2. f(x)的图象略.
(2)由(1)知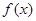 =
=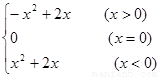 ,由图象可知,
,由图象可知,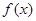 在[-1,1]上单调递增,要使
在[-1,1]上单调递增,要使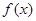 在[-1,
在[-1, -2]上单调递增,只需
-2]上单调递增,只需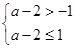 解之得
解之得 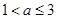
考点:本题主要是考查奇函数的定义,函数的图像与函数单调性的关系的运用,属中档题.。
点评:解决该试题的关键是应用转化的思想求值;作函数的图象,求a的取值范围,体现了作图和用图的能力。


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com