
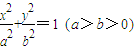 的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.
的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.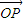 •
•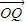 =
= b2.
b2.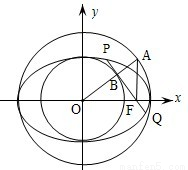
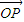 •
•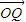 整理可得结论.(注意整理过程中要细心)
整理可得结论.(注意整理过程中要细心)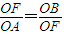 ,即
,即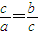 ,因此c2=ab.①(2分)
,因此c2=ab.①(2分)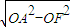 =
=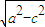 =b
=b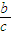 .设直线BF的斜率为k,k=-
.设直线BF的斜率为k,k=-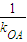 =-
=-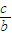 .
.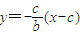 (5分)
(5分)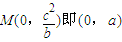 .(6分)
.(6分)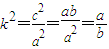 ②
②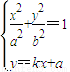 ③
③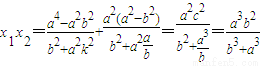 .
.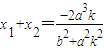
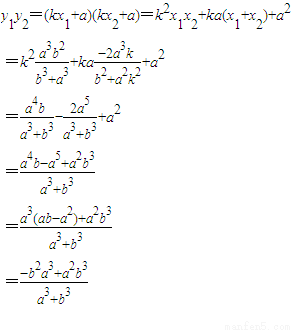
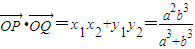 ,(12分)
,(12分)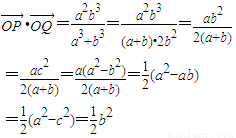 (15分)
(15分)

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
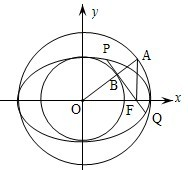 如图,以椭圆
如图,以椭圆| x2 |
| a2 |
| y2 |
| b2 |
| OP |
| OQ |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年天津卷理)(14分)
如图,以椭圆![]() 的中心O为圆心,分别以
的中心O为圆心,分别以![]() 和
和![]() 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点![]() 作垂直于
作垂直于![]() 轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。
轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。

(I)证明![]() 并求直线BF与
并求直线BF与![]() 同的交点M的坐标;
同的交点M的坐标;
(II)设直线BF交椭圆P、Q两点,证明![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
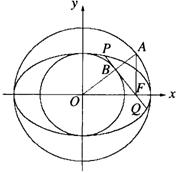
(Ⅰ)证明c2=ab,并求直线BF与y轴的交点M的坐标;
(Ⅱ)设直线BF交椭圆于P、Q两点,证明![]() ·
·![]() =
=![]() b2.
b2.
查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷05(文科)(解析版) 题型:解答题
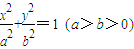 的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.
的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.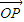 •
•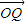 =
= b2.
b2.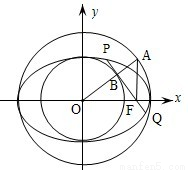
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com