Question

9．如图所示，四棱锥P-ABCD的底面为等腰梯形，AB∥DC，AB=2AD=2，PA⊥平面ABCD，∠ABC=60°
（1）求AC的长；
（2）证明：BC⊥PC；
（3）若PA=AB，求PC与平面PAD所成角的正弦值．

Answer 1

分析 （1）由已知条件利用余弦定理能求出AC．
（2）首先利用中点得到△BCE为正三角形，进一步利用勾股定理的逆定理得到线线垂直，再利用线面垂直的判定定理证得：线面垂直．最后转化成面面垂直．
（3）首先作出直线与平面的夹角的平面角，进一步利用解直角三角形知识求得结果．

解答 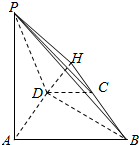解：（1）∵四棱锥P-ABCD的底面为等腰梯形，
AB∥DC，AB=2AD=2，PA⊥平面ABCD，∠ABC=60°，
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2×AB×BC×cos60°}$
=$\sqrt{4+1-2×2×1×\frac{1}{2}}$
=$\sqrt{3}$．
证明：（2）取AB的中点，连接CE，则由题意知：△BCE为正三角形，
∵∠ABC=60°，
∴由等腰梯形知：∠BCD=120°，∵AD=CD=BC=1，AB=4，BD=AC=$\sqrt{3}$，
∴AD²+BD²=AB²，∴∠ADB=90°，∴AD⊥BD，
又∵PA⊥平面ABCD，∴PA⊥BD，
∴BD⊥平面PAD，且BC?平面PBD，
∴平面PBD⊥平面PAD．
解：（3）在平面ABCD中，过点C作CH∥BD交AD的延长线于点H，
由（2）知：BD⊥平面PAD，∴CH⊥平面PAD，
连接PH，则∠CPH即为PC与平面PAD所成角．
在Rt△CHD中，CD=1，∠CDH=60°，
∴CH=$\frac{1}{2}\sqrt{3}$，在Rt△PHC中，PC=$\sqrt{P{A}^{2}+A{C}^{2}}$=$\sqrt{7}$，
∴在Rt△PHC中，sin∠CPH=$\frac{CH}{PC}$=$\frac{\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{\sqrt{21}}{14}$．
∴直线PC与平面PAD所成角的正弦值为$\frac{\sqrt{21}}{14}$．

点评 本题考查的知识要点：勾股定理逆定理的应用，现面向垂直的判定和性质定理的应用，面面垂直的判定定理的应用，线面的夹角的应用．主要考查学生的空间想象能力和应用能力．