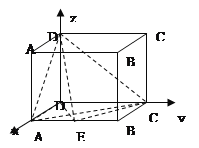
[题目]如图.长方体中...点E是线段AB中点．证明:,求二面角的大小的余弦值,求A点到平面的距离．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】如图，长方体中，，，点E是线段AB中点．

证明：；

求二面角的大小的余弦值；

求A点到平面的距离．

【答案】（1）详见解析（2）（3）

【解析】

试题（1）面，，，又，[来所以，面所以，（2）是所求二面角的平面角，，，二面角的大小的余弦值为（3）由（１）（２）知，平面的法向量为，

试题解析：（1）证明：面，面

所以，１分

中，，

同理：，又，

3分

所以，面4分

又面

所以，5分

（2）解法一由（1）证可知是所求二面角的平面角６分

在中，，；

故，8分

即二面角的大小的余弦值为9分

解法二：利用向量法

设平面的法向量为，

由（1）得，

且

解得：,即； 7分

又平面的法向量为，

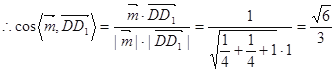
所以，二面角的余弦值为． 9分

（3）解法一：，，，

10分

又，，，

（11分）

设点到平面的距离为，则，

解得，即点到平面的距离为．（14分）

解法二：利用向量法

由（1）（2）知，平面的法向量为

故，点到平面的距离为

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】为激发学生学习的兴趣，老师上课时在黑板上写出三个集合：；然后叫甲、乙、丙三位同学到讲台上，并将“”中的数告诉了他们，要求他们各用一句话来描述，以便同学们能确定该数，以下是甲、乙、丙三位同学的描述：

甲：此数为小于6的正整数；乙：A是B成立的充分不必要条件；

丙：A是C成立的必要不充分条件

若老师评说这三位同学都说得对，则“”中的数为。

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】求满足下列条件的抛物线的标准方程.

(1)过点.

(2)焦点在直线上.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在矩形中，点在线段上，，，沿直线将翻折成，使点在平面上的射影落在直线上.

（Ⅰ）求证：直线平面；

（Ⅱ）求二面角的平面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】用,,表示空间中三条不同的直线,表示平面, 给出下列命题:

① 若,, 则∥; ② 若∥,∥, 则∥;

③ 若∥,∥, 则∥; ④ 若 , , 则∥.

其中真命题的序号是（）

A. ①② B. ②③ C. ①④ D. ②④

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线上一点到其焦点的距离为，以为圆心且与抛物线准线相切的圆恰好过原点.点是与轴的交点，两点在抛物线上且直线过点，过点及的直线交抛物线于点.

（1）求抛物线的方程；

（2）求证：直线过一定点，并求出该点坐标.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】朱载堉（1536—1611），明太祖九世孙，音乐家、数学家、天文历算家，在他多达百万字的著述中以《乐律全书》最为著名，在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”，此理论被广泛应用在世界各国的键盘乐器上，包括钢琴，故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音，相邻两个音之间的频率之比相等，且最后一个音频率是最初那个音频率的2倍，设第二个音的频率为，第八个音的频率为，则等于