解:(1)∵△ABC的面积为2

,

•

=4,
∴

bcsinA=2

①,bccosA=4②,
①÷②得:tanA=

,
又A为三角形的内角,
则A=

;
(2)法1:∵A=

,∴B+C=

,即C=

-B,
∴根据正弦定理得:
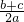
=
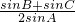
=
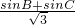
=

[sinB+sin(

-B)]
=

(

cosB+

sinB)=sin(B+

),
∵0<B<

,∴

<B+

<

,
∴当B+

=

,即B=

时,sin(B+

)取得最大值1,
则
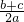
的最大值是1;
法2:∵cosA=

,
∴由余弦定理得:a
2=b
2+c
2-2bccosA=(b+c)
2-3bc≥(b+c)
2-3(
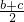
)
2=

(b+c)
2,
整理得:(
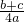
)
2≤1,即
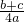
≤1,
则当b=c时,
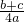
最大值是1.
分析:(1)利用三角形的面积公式表示出三角形ABC的面积,将已知的面积代入得到一个关系式,记作①,利用平面向量的数量积运算法则化简

•

=4,得到另一个关系式,记作②,①÷②,利用同角三角函数间的基本关系弦化切,求出tanA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
(2)法1:由A的度数,求出B+C的度数,用B表示出C,利用正弦定理化简所求的式子,将sinA的值代入,并将表示出的C代入,整理后利用两角和与差的正弦函数公式化为一个角的正弦函数,由B的范围求出这个角的范围,利用正弦函数的图象与性质求出正弦函数的最大值,即为所求式子的最大值;
法2:由A的度数得出cosA的值,利用余弦定理得到a
2=b
2+c
2-2bccosA,将cosA的值代入并利用完全平方公式变形,再利用基本不等式化简,变形后求出所求式子的范围,即可得到所求式子的最大值.
点评:此题属于解三角形的题型,涉及的知识有:正弦、余弦定理,三角形的面积公式,平面向量的数量积运算法则,三角函数的恒等变形,以及基本不等式的运用,熟练掌握定理及公式是解本题的关键.

 ,角A,B,C的对边分别为a,b,c,
,角A,B,C的对边分别为a,b,c, •
• =4.
=4.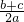 的最大值.
的最大值. ,
, •
• =4,
=4, bcsinA=2
bcsinA=2 ①,bccosA=4②,
①,bccosA=4②, ,
, ;
; ,∴B+C=
,∴B+C= ,即C=
,即C= -B,
-B,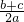 =
=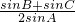 =
=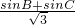 =
= [sinB+sin(
[sinB+sin( -B)]
-B)] (
( cosB+
cosB+ sinB)=sin(B+
sinB)=sin(B+ ),
), ,∴
,∴ <B+
<B+ <
< ,
, =
= ,即B=
,即B= 时,sin(B+
时,sin(B+ )取得最大值1,
)取得最大值1,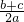 的最大值是1;
的最大值是1; ,
,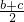 )2=
)2= (b+c)2,
(b+c)2,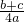 )2≤1,即
)2≤1,即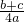 ≤1,
≤1,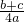 最大值是1.
最大值是1. •
• =4,得到另一个关系式,记作②,①÷②,利用同角三角函数间的基本关系弦化切,求出tanA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;
=4,得到另一个关系式,记作②,①÷②,利用同角三角函数间的基本关系弦化切,求出tanA的值,由A为三角形的内角,利用特殊角的三角函数值即可求出A的度数;

 名校课堂系列答案
名校课堂系列答案 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 (2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.
(2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.