
(本题共10分)
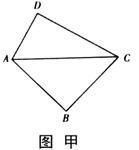
将两块三角板按图甲方式拼好,其中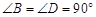 ,
,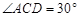 ,
,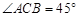 ,
,
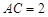 ,现将三角板
,现将三角板 沿
沿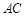 折起,使
折起,使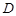 在平面
在平面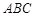 上的射影恰好在
上的射影恰好在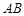 上,如图乙.
上,如图乙.
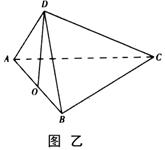
(Ⅰ)求证: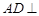 平面
平面 ;
;
(Ⅱ)求二面角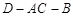 的余弦值;
的余弦值;
(1)见解析;(2)二面角的余弦值为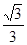 。
。
【解析】本试题主要是考查了线面的垂直的证明以及二面角的求解的综合运用。
(1)根据已知条件,可知设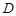 在
在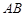 的射影为
的射影为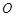 ,则
,则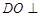 平面
平面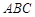 ,
,
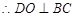 , 又
, 又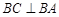 ,
, 平面
平面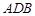
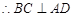 ,又
,又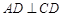 ,这样利用线线垂直可知得到结论。
,这样利用线线垂直可知得到结论。
(2)建立空间直角坐标系,然后分析点的坐标和向量的坐标,运用向量的夹角来求解两个平面的二面角的平面角的大小。
解:(1)设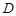 在
在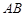 的射影为
的射影为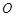 ,则
,则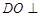 平面
平面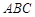 ,
,
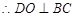 , 又
, 又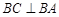 ,
, 平面
平面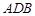
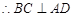 ,又
,又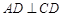 ,
,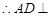 平面
平面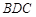 ……………………4分
……………………4分
(2)由(1)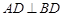 ,又
,又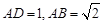 ,
,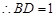
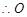 为
为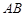 中点
中点
以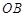 为
为 轴,
轴,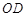 为
为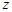 轴,过
轴,过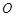 且与
且与 平行的直线为
平行的直线为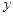 轴建系,则
轴建系,则

设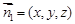 为平面
为平面 的法向量,由
的法向量,由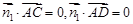 ,可得
,可得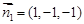
易知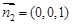 为平面
为平面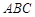 的法向量,
的法向量,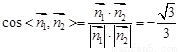
因为所求二面角是锐角,所以所求二面角的余弦值为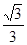 。…………………10分
。…………………10分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
(本题满分共12分)某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究,他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪,然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数,得到如下资料:
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温 差 | 10 | 13 | 11 | 12 | 7 |
| 感染数 | 23 | 32 | 24 | 29 | 17 |
(1)求这5天的平均感染数;(2)从4月1日至4月5日中任取2天,记感染数分别为![]() 用
用![]() 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中![]() 视为同一事件,并求
视为同一事件,并求![]() 的事件A的概率。
的事件A的概率。
查看答案和解析>>
科目:高中数学 来源:2013届山东冠县武训高中高二下第三次模块考试理科数学试题(解析版) 题型:解答题
(本题共10分)
将两块三角板按图甲方式拼好,其中 ,
, ,
, ,
,

 ,现将三角板
,现将三角板 沿
沿 折起,使
折起,使 在平面
在平面 上的射影恰好在
上的射影恰好在 上,如图乙.
上,如图乙.

(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市黄浦区高三上学期期终基础学业测评理科数学试卷 题型:解答题
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点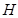 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点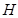 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com